Question

【题目】已知椭圆．

（1）若椭圆的离心率为，求的值；

（2）若过点任作一条直线与椭圆交于不同的两点，在轴上是否存在点，使得 若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）=；（2）存在点 ，使得 ．

【解析】

（1）由a2=2，b2=n，所以c2=2-n，又，得n
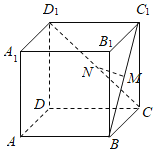
（2）若存在点M（m，0），使得∠NMA+∠NMB=180°，
则直线AM和BM的斜率存在，分别设为k1，k2．等价于k1+k2=0．
依题意，直线l的斜率存在，故设直线l的方程为y=k（x+2）．与椭圆方程联立，利用△＞0．求出．设A（x1，y1），B（x2，y2），利用韦达定理，通过令，求出m．

解：（1） 因为 ，，所以 ．

又 ，所以有 ，得 ．

（2）若存在点 ，使得 ，

则直线 和 的斜率存在，

分别设为 ，，且满足 ．

依题意，直线 的斜率存在，故设直线 的方程为 ．

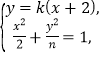由 得 ．

因为直线 与椭圆 有两个交点，所以 ．

即 ，解得 ．

设 ，，则 ，，

，．

令 ，即 ，

即 ，

当 时，，

所以 ，化简得，，所以 ．

当 时，检验也成立．

所以存在点 ，使得 ．