╠Ô─┐─┌╚Ţ
 ĎĐͬ═Íď▓C1ú║
ĎĐͬ═Íď▓C1ú║| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
úĘ1úęăˇ═Íď▓C1Á─ĚŻ│╠ú╗
úĘ2úęÁŃN╩ă═Íď▓Á─Ρ¹ÁŃúČÁŃP╩ă═Íď▓C1╔¤▓╗═ČË┌ÁŃNÁ─╚╬ĎÔĎ╗ÁŃúČ┴ČŻË
NP▓óĐË│ĄŻ╗═Íď▓ËĎÎ╝¤▀ËŰÁŃTúČăˇ
| TP |
| NP |
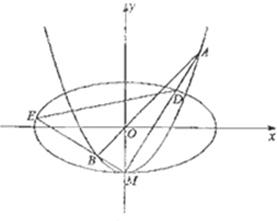
úĘ3úę╔Ŕă˙¤▀C2ú║y=x2-1ËŰyÍßÁ─Ż╗ÁŃ╬¬MúČ╣řMθ┴Ż╠§╗ą¤Ó┤╣Í▒Á─Í▒¤▀ËŰă˙¤▀C2íó═Íď▓C1¤ÓŻ╗Ë┌ÁŃAíóD║═BíóEúČúĘ╚š═╝úęúČ╝ăí¸MABíó
í¸MDEÁ─├Š╗řĚÍ▒╩ăS1úČS2úČÁ▒
| S1 |
| S2 |
| 27 |
| 64 |
ĚÍ╬÷ú║úĘ1úę¤╚└űË├└Űđ─┬╩║═Ż╣ÁŃΰ▒ŕúČÁ├ÁŻĎ╗Ş÷╣ěË┌▓╬╩řÁ─ĚŻ│╠ÎÚúČŻÔŇÔŞ÷ĚŻ│╠ÎÚ╝┤┐╔ăˇ│÷▓╬╩řúČŻ°Â°ăˇ│÷═Íď▓C1Á─ĚŻ│╠ú«
úĘ2úęË╔╠Ô╔Ŕ╠§╝■đđăˇ│÷NúĘ-2úČ0úęúČ═Íď▓ËĎÎ╝¤▀ú║x=
úČ╔ŔPúĘxúČyúęúČď˛
=
úČď┘Ë╔-2í▄xí▄2úČ─▄ăˇ│÷
Á─╚íÍÁĚÂ╬žú«
úĘ3úę¤╚░ĐÍ▒¤▀MAÁ─ĚŻ│╠ËŰ┼Î╬´¤▀ĚŻ│╠┴¬┴ó┐╔Á├ÁŃAÁ─ΰ▒ŕúČď┘└űË├¤Ď│Ą╣ź╩Żăˇ│÷|MA|úČ═ČШÁ─ĚŻĚĘăˇ│÷|MB|Ż°Â°ăˇ│÷S1úČ═Č└Ý┐╔ăˇS2ú«ď┘┤˙╚ŰĎĐͬż═┐╔ͬÁ└╩ăĚ˝┤Šď┌Í▒¤▀l┬˙ÎŃ╠ÔÍđ╠§╝■┴╦ú«
úĘ2úęË╔╠Ô╔Ŕ╠§╝■đđăˇ│÷NúĘ-2úČ0úęúČ═Íď▓ËĎÎ╝¤▀ú║x=
4
| ||
| 3 |
| TP |
| NP |
| ||||
| x+2 |
| TP |
| NP |
úĘ3úę¤╚░ĐÍ▒¤▀MAÁ─ĚŻ│╠ËŰ┼Î╬´¤▀ĚŻ│╠┴¬┴ó┐╔Á├ÁŃAÁ─ΰ▒ŕúČď┘└űË├¤Ď│Ą╣ź╩Żăˇ│÷|MA|úČ═ČШÁ─ĚŻĚĘăˇ│÷|MB|Ż°Â°ăˇ│÷S1úČ═Č└Ý┐╔ăˇS2ú«ď┘┤˙╚ŰĎĐͬż═┐╔ͬÁ└╩ăĚ˝┤Šď┌Í▒¤▀l┬˙ÎŃ╠ÔÍđ╠§╝■┴╦ú«
ŻÔ┤ú║ŻÔú║úĘ1úęí▀═Íď▓C1ú║
+
=1(aúżbúż0)Á─└Űđ─┬╩╬¬
úČ
Ď╗Ş÷Ż╣ÁŃΰ▒ŕ╬¬F(-
úČ0)úČ
íÓ
úČ
íÓa=2úČc=
úČb=
=1úČ
íÓ═Íď▓C1Á─ĚŻ│╠╬¬ú║
+y2=1ú«
úĘ2úęí▀N╩ă═Íď▓C1ú║
+y2=1Á─Ρ¹ÁŃúČÁŃP╩ă═Íď▓C1╔¤▓╗═ČË┌ÁŃNÁ─╚╬ĎÔĎ╗ÁŃúČ
íÓNúĘ-2úČ0úęúČ═Íď▓ËĎÎ╝¤▀ú║x=
úČ
╔ŔPúĘxúČyúęúČď˛
=
úČ
í▀-2í▄xí▄2úČ
íÓ
=
í╩[
úČ+íŮúęú«
╣╩
Á─╚íÍÁĚÂ╬ž╩ă[
úČ+íŮúęú«
úĘ3úę╔ŔÍ▒¤▀MAÁ─đ▒┬╩╬¬k1úČď˛Í▒¤▀MAÁ─ĚŻ│╠╬¬y=k1x-1ú«
Ë╔
úČŻÔÁ├
úČ╗˛
ú«
ď˛ÁŃAÁ─ΰ▒ŕ╬¬úĘk1úČk12-1úęú«
ËÍÍ▒¤▀MBÁ─đ▒┬╩╬¬-
úČ═Č└Ý┐╔Á├ÁŃBÁ─ΰ▒ŕ╬¬úĘ-
úČ
-1úęú«
Ë┌╩ăS1=
|MA|•|MB|=
•|k1|•
•|-
|=
ú«
Ë╔
úČÁ├úĘ1+4k12úęx2-8k1x=0ú«
ŻÔÁ├
úČ╗˛
úČď˛ÁŃDÁ─ΰ▒ŕ╬¬úĘ
úČ
úęú«
ËÍÍ▒¤▀MEÁ─đ▒┬╩╬¬-
ú«═Č└Ý┐╔Á├ÁŃEÁ─ΰ▒ŕ╬¬úĘ
úČ
úęú«
Ë┌╩ăS2=
|MD|•|ME|=
ú«
╣╩
=
(4k12+
+17)=
úČŻÔÁ├k12=2úČ╗˛k12=
ú«
ËÍË╔ÁŃAúČBÁ─ΰ▒ŕÁ├úČk=
=k1-
ú«╦¨Ďďk=í└
ú«
╣╩┬˙ÎŃ╠§╝■Á─Í▒¤▀┤Šď┌úČăĎËđ┴Ż╠§úČĂńĚŻ│╠╬¬y=
x║═y=-
xú«
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
Ď╗Ş÷Ż╣ÁŃΰ▒ŕ╬¬F(-
| 3 |
íÓ
|
íÓa=2úČc=
| 3 |
| 4-3 |
íÓ═Íď▓C1Á─ĚŻ│╠╬¬ú║
| x2 |
| 4 |
úĘ2úęí▀N╩ă═Íď▓C1ú║
| x2 |
| 4 |
íÓNúĘ-2úČ0úęúČ═Íď▓ËĎÎ╝¤▀ú║x=
4
| ||
| 3 |
╔ŔPúĘxúČyúęúČď˛
| TP |
| NP |
| ||||
| x+2 |
í▀-2í▄xí▄2úČ
íÓ
| TP |
| NP |
| ||||
| x+2 |
2
| ||
| 6 |
╣╩
| TP |
| NP |
2
| ||
| 6 |
úĘ3úę╔ŔÍ▒¤▀MAÁ─đ▒┬╩╬¬k1úČď˛Í▒¤▀MAÁ─ĚŻ│╠╬¬y=k1x-1ú«
Ë╔
|
|
|
ď˛ÁŃAÁ─ΰ▒ŕ╬¬úĘk1úČk12-1úęú«
ËÍÍ▒¤▀MBÁ─đ▒┬╩╬¬-
| 1 |
| k1 |
| 1 |
| k1 |
| 1 |
| k12 |
Ë┌╩ăS1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k12 |
1+
|
| 1 |
| k1 |
| 1+k12 |
| 2|k1| |
Ë╔
|
ŻÔÁ├
|
|
| 8k1 |
| 1+4k12 |
| 4k12-1 |
| 1+4k12 |
ËÍÍ▒¤▀MEÁ─đ▒┬╩╬¬-
| 1 |
| k1 |
| -8k1 |
| 1+4k12 |
| 4-k12 |
| 4+k12 |
Ë┌╩ăS2=
| 1 |
| 2 |
| 32(1+k12)•|k1| |
| (1+4k12)(k12+4) |
╣╩
| S1 |
| S2 |
| 1 |
| 64 |
| 4 |
| k12 |
| 27 |
| 64 |
| 1 |
| 2 |
ËÍË╔ÁŃAúČBÁ─ΰ▒ŕÁ├úČk=
k12-
| ||
k1+
|
| 1 |
| k1 |
| ||
| 2 |
╣╩┬˙ÎŃ╠§╝■Á─Í▒¤▀┤Šď┌úČăĎËđ┴Ż╠§úČĂńĚŻ│╠╬¬y=
| ||
| 2 |
| ||
| 2 |
ÁŃĂ└ú║▒ż╠Ô╩ăÂď═Íď▓ËŰ┼Î╬´¤▀Ďď╝░Í▒¤▀ËŰ┼Î╬´¤▀║═Í▒¤▀ËŰ═Íď▓Á─Î█║¤╬╩╠ÔÁ─┐╝▓Úú«╩ăĎ╗Á└Ňű└Ý╣ř│╠║▄┬ÚĚ│Á─╠ÔúČđŔϬϬ╚¤ŇŠúȤŞÍ┬Á─╠ČÂ╚▓┼─▄░Đ╠Ô─┐θ║├ú«

┴̤░▓ߤÁ┴đ┤░Ş
 └°ď┼╩ÚĎÁ╩ţ╝┘¤╬ŻË─■▓Ę│÷░Š╔š¤Á┴đ┤░Ş
└°ď┼╩ÚĎÁ╩ţ╝┘¤╬ŻË─■▓Ę│÷░Š╔š¤Á┴đ┤░Ş
¤Ó╣ě╠Ô─┐
 ĎĐͬ═Íď▓
ĎĐͬ═Íď▓