题目内容
设x，y，z∈R，且满足：x2＋y2＋z2＝1，x＋2y＋3z＝
，则x＋y＋z＝________.
【解析】由柯西不等式，得
(x2＋y2＋z2)(12＋22＋32)≥(x＋2y＋3z)2，
∴(x＋2y＋3z)2≤14，则x＋2y＋3z≤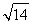
，
又x＋2y＋3z＝
，
∴x＝
，
因此x＝
，y＝
，z＝
，
于是x＋y＋z＝
.
练习册系列答案
相关题目
题目内容
设x，y，z∈R，且满足：x2＋y2＋z2＝1，x＋2y＋3z＝，则x＋y＋z＝________.
【解析】由柯西不等式，得
(x2＋y2＋z2)(12＋22＋32)≥(x＋2y＋3z)2，
∴(x＋2y＋3z)2≤14，则x＋2y＋3z≤，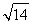
又x＋2y＋3z＝，
∴x＝，
因此x＝，y＝，z＝，
于是x＋y＋z＝.
