题目内容
数列{an}的前n项和记为Sn,且满足Sn=2an-1.
(1)求数列{an}的通项公式;
(2)求和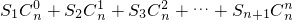 ;
;
(3)设有m项的数列{bn}是连续的正整数数列,并且满足: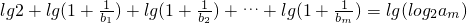 .
.
问数列{bn}最多有几项?并求这些项的和.
解:(1)由Sn=2an-1得Sn+1=2an+1-1,相减得an+1=2an+1-2an,即an+1=2an.
又S1=2a1-1,得a1=1≠0,
∴数列{an}是以1为首项2为公比的等比数列,
∴an=2n-1.
(2)由(1)知Sn=2n-1,
∴S1• +S2•
+S2• +S3•
+S3• +…+Sn+1•
+…+Sn+1•
=(21-1)• +(22-1)•
+(22-1)• +(23-1)•
+(23-1)• +…+(2n+1-1)•
+…+(2n+1-1)•
=2( +2
+2 +22
+22 +…+2n
+…+2n )-(
)-( +
+ +
+ +…+
+…+ )
)
=2(1+2)n-2n
=2•3n-2n
(3)由已知得2•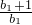 •
•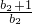 …
…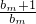 =m-1.
=m-1.
又{bn}是连续的正整数数列,
∴bn=bn-1+1.
∴上式化为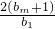 =m-1.
=m-1.
又bm=b1+(m-1),消bm得mb1-3b1-2m=0.
m=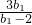 =3+
=3+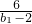 ,由于m∈N*,
,由于m∈N*,
∴b1>2,
∴b1=3时,m的最大值为9.
此时数列的所有项的和为3+4+5+…+11=63
分析:(1)利用an+1=Sn+1-Sn,即可求得an+1=2an.,继而可证明数列{an}为等比数列,利用等比数列的概念即可求数列{an}的通项公式;
(2)由(1)知Sn=2n-1,将其代入S1• +S2•
+S2• +S3•
+S3• +…+Sn+1•
+…+Sn+1• ,分组求和.利用二项式定理即可求得其结果;
,分组求和.利用二项式定理即可求得其结果;
(3)利用对数的性质可得到2•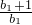 •
•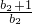 …
…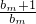 =m-1,利用{bn}是连续的正整数数列,且满足上式,可化为
=m-1,利用{bn}是连续的正整数数列,且满足上式,可化为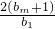 =m-1,利用bm=b1+(m-1),消bm即可求得答案.
=m-1,利用bm=b1+(m-1),消bm即可求得答案.
点评:本题考查二项式定理的应用,考查数列求和,考查数列递推式,突出考查创新思维与抽象逻辑思维的能力,属于难题.
又S1=2a1-1,得a1=1≠0,
∴数列{an}是以1为首项2为公比的等比数列,
∴an=2n-1.
(2)由(1)知Sn=2n-1,
∴S1•
 +S2•
+S2• +S3•
+S3• +…+Sn+1•
+…+Sn+1•
=(21-1)•
 +(22-1)•
+(22-1)• +(23-1)•
+(23-1)• +…+(2n+1-1)•
+…+(2n+1-1)•
=2(
 +2
+2 +22
+22 +…+2n
+…+2n )-(
)-( +
+ +
+ +…+
+…+ )
)=2(1+2)n-2n
=2•3n-2n
(3)由已知得2•
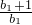 •
•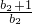 …
…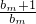 =m-1.
=m-1.又{bn}是连续的正整数数列,
∴bn=bn-1+1.
∴上式化为
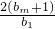 =m-1.
=m-1.又bm=b1+(m-1),消bm得mb1-3b1-2m=0.
m=
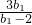 =3+
=3+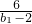 ,由于m∈N*,
,由于m∈N*,∴b1>2,
∴b1=3时,m的最大值为9.
此时数列的所有项的和为3+4+5+…+11=63
分析:(1)利用an+1=Sn+1-Sn,即可求得an+1=2an.,继而可证明数列{an}为等比数列,利用等比数列的概念即可求数列{an}的通项公式;
(2)由(1)知Sn=2n-1,将其代入S1•
 +S2•
+S2• +S3•
+S3• +…+Sn+1•
+…+Sn+1• ,分组求和.利用二项式定理即可求得其结果;
,分组求和.利用二项式定理即可求得其结果;(3)利用对数的性质可得到2•
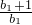 •
•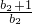 …
…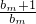 =m-1,利用{bn}是连续的正整数数列,且满足上式,可化为
=m-1,利用{bn}是连续的正整数数列,且满足上式,可化为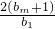 =m-1,利用bm=b1+(m-1),消bm即可求得答案.
=m-1,利用bm=b1+(m-1),消bm即可求得答案.点评:本题考查二项式定理的应用,考查数列求和,考查数列递推式,突出考查创新思维与抽象逻辑思维的能力,属于难题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目