题目内容
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若对任意的![]() ,
,![]() ,都有
,都有![]() 恒成立,试求m的取值范围;
恒成立,试求m的取值范围;
(2)用![]() 表示m,n中的最小值,设函数
表示m,n中的最小值,设函数![]() (
(![]() ),讨论关于x的方程
),讨论关于x的方程![]() 的实数解的个数.
的实数解的个数.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据![]() 恒成立转化为
恒成立转化为![]() 恒成立,即来研究函数
恒成立,即来研究函数![]() 的最值,再分当
的最值,再分当![]() ,
,![]() ,
,![]() 时三种情况分分类讨论求解.
时三种情况分分类讨论求解.
(2) 将方程![]() 的实数解的个数,转化为函数
的实数解的个数,转化为函数![]() 零点的个数问题来研究,根据函数
零点的个数问题来研究,根据函数![]() 的定义,分
的定义,分![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 三种情况下,对
三种情况下,对![]() 讨论.
讨论.
(1)![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
所以![]() ,
,
解得![]() ,不合题意舍去,
,不合题意舍去,
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
而![]() ,
,![]() ,
,
所以有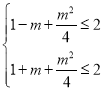 ,
,
解得![]() ,即
,即![]() ,
,
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,
,
![]() ,
,
解得![]() ,不合题意,
,不合题意,
.综上所述,m的取值范围为![]() .
.
(2)方程![]() 的实数解的个数
的实数解的个数![]() 函数
函数![]() 零点的个数.
零点的个数.
①当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上没有零点,即方程
上没有零点,即方程![]() 在
在![]() 上没有实数解;
上没有实数解;
②当![]() 时,
时,![]() ,
,![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() ,所以
,所以![]() 是函数
是函数![]() 的零点,
的零点,
即方程![]() 有一实数解
有一实数解![]() ,
,
若![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() 此时不是函数
此时不是函数![]() 的零点,
的零点,
即方程![]() 此时无实数解;
此时无实数解;
.③当![]() 时,
时,![]() ,所以只需考虑
,所以只需考虑![]() 在
在![]() 上的零点个数,
上的零点个数,
则由![]() 得
得![]() ,
,![]() 即问题等价于直线
即问题等价于直线![]() 与函数
与函数![]() ,
,![]() 图象的交点的个数.
图象的交点的个数.
由于对勾函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
结合![]() ,
,![]() 的图象可知,
的图象可知,
当![]() 时,
时,![]() 与函数
与函数![]() ,
,![]() 的图象没有交点,
的图象没有交点,
即函数![]() 在
在![]() 上没有零点,即方程
上没有零点,即方程![]() 在
在![]() 上没有实数解;
上没有实数解;
当![]() 或
或![]() 时,
时,![]() 在
在![]() 上有一个实数解;
上有一个实数解;
当![]() 时,
时,![]() 在
在![]() 上有两个实数解;
上有两个实数解;
综上所述,当![]() 或
或![]() 时,方程
时,方程![]() 有一个实数解,
有一个实数解,
当![]() 或
或![]() 时,方程
时,方程![]() 在
在![]() 上有两个实数解,
上有两个实数解,
当![]() 时,方程
时,方程![]() 在
在![]() 上有三个实数解.
上有三个实数解.

【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 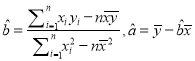 .
.