题目内容
若函数y=f(x)对定义域的每一个值x1,都存在唯一的x2,使y=f(x1)f(x2)=1成立,则 称此函数为“滨湖函数”.下列命题正确的是 .(把你认为正确的序号都填上)①y=
 是“滨湖函数”;
是“滨湖函数”;②y=
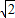 +sinx(x∈[
+sinx(x∈[ ])I是“滨湖函数”;
])I是“滨湖函数”;③y=2x是“滨湖函数”;
④y=lnx是“滨湖函数”;
⑤y=f(x),y=g(x)都是“滨湖函数”,且定义域相同,则y=f(x)g(x)是“滨湖函数”
【答案】分析:利用“滨湖函数”的定义,逐个分析①②③④⑤五个函数,能够得到结果.
解答:解:对于①,对应的x1,x2不唯一,
∴①不一定是“滨湖函数”;
对于②,函数y=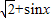 是[-
是[-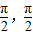 ]上的单调增函数,
]上的单调增函数,
对[-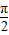 ,
,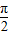 ]内的每一个值
]内的每一个值 ∈[
∈[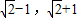 ],
],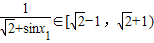 ,
,
∴在[-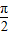 ,
,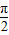 ]内存在唯一的x2,使
]内存在唯一的x2,使 =
=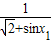 ∈[
∈[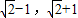 ]成立,
]成立,
∴②是“滨湖函数”;
对于③,∵y=2x,2x•2-x=1,
∴③是“滨湖函数”;
对于④,y=lnx有零点,∴④一定不是y=lnx“滨湖函数”;
对于⑤,∵y=f(x),y=g(x)都是“滨湖函数”,且定义域相同,
∴对于定义域中每一个x1,都存在唯一的x2,使y=f(x1)f(x2)=1和y=g(x1)g(x2)=1成立,
∵两个x2不一定相等,
∴y=f(x1)g(x1)•f(x2)g(x2)=1不一定成立,
∴⑤不是“滨湖函数”.
故答案为:②③.
点评:本题考查函数的性质的基本应用,解题时要认真审题,注意理解“滨湖函数”的概念.
解答:解:对于①,对应的x1,x2不唯一,
∴①不一定是“滨湖函数”;
对于②,函数y=
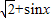 是[-
是[-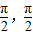 ]上的单调增函数,
]上的单调增函数,对[-
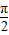 ,
,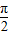 ]内的每一个值
]内的每一个值 ∈[
∈[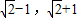 ],
],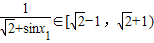 ,
,∴在[-
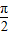 ,
,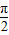 ]内存在唯一的x2,使
]内存在唯一的x2,使 =
=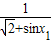 ∈[
∈[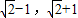 ]成立,
]成立,∴②是“滨湖函数”;
对于③,∵y=2x,2x•2-x=1,
∴③是“滨湖函数”;
对于④,y=lnx有零点,∴④一定不是y=lnx“滨湖函数”;
对于⑤,∵y=f(x),y=g(x)都是“滨湖函数”,且定义域相同,
∴对于定义域中每一个x1,都存在唯一的x2,使y=f(x1)f(x2)=1和y=g(x1)g(x2)=1成立,
∵两个x2不一定相等,
∴y=f(x1)g(x1)•f(x2)g(x2)=1不一定成立,
∴⑤不是“滨湖函数”.
故答案为:②③.
点评:本题考查函数的性质的基本应用,解题时要认真审题,注意理解“滨湖函数”的概念.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目