题目内容
下列命题:①G2=ab是三个数a、G、b成等比数列的充要条件;
②若函数y=f(x)对任意实数x都满足f(x+2)=-f(x),则f(x)是周期函数;
③对于命题p:?x∈R,2x+3>0,则?p:?x∈R,2x+3<0;
④直线
| 2 |
其中不正确命题的序号为
分析:令a=b=G=0虽然符合G2=ab,不成等比数列判断出,①不正确;根据f(x+2)=-f(x)=f(x-2)求得函数的周期为4,判断出函数为周期函数判断出.②正确;命题?p:?x0∈R,2x0+3≤0,进而判断出③不正确.求得圆心到直线的距离大于或等于半径判断出,④不正确.
解答:解:当a=b=G=0时,G2=ab,但是a,G,b不构成等比数列,①不正确,
②f(x+2)=-f(x)=f(x-2),∴T=4,f(x)为周期函数.②正确;
③命题?p:?x0∈R,2x0+3≤0,因此,③不正确.
④圆心(0,0)到直线
(x+y)+1+a=0的距离为
大于或等于圆的半径
,④不正确.
故答案为:①③④
②f(x+2)=-f(x)=f(x-2),∴T=4,f(x)为周期函数.②正确;
③命题?p:?x0∈R,2x0+3≤0,因此,③不正确.
④圆心(0,0)到直线
| 2 |
| 1+a |
| 2 |
| a |
故答案为:①③④
点评:本题主要考查了直线与圆的位置关系,函数基础知识的综合运用.等比数列的判定等.考查了学生综合运用所学知识的能力.

练习册系列答案
相关题目
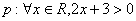 ,则
,则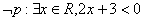 ;
;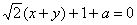 与圆C:x2+y2=a(a>0)相离.
与圆C:x2+y2=a(a>0)相离. ,则
,则 ;④直线
;④直线 与圆C:x2+y2=a(a>0)相离.
与圆C:x2+y2=a(a>0)相离.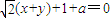 与圆C:x2+y2=a(a>0)相离.
与圆C:x2+y2=a(a>0)相离.