题目内容
(满分13分)
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.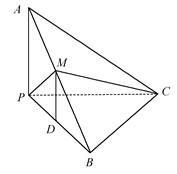
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(1)要证DM∥平面APC,只需证明MD∥AP(因为AP?面APC)即可.
(2)在平面ABC内直线AP⊥BC,BC⊥AC,即可证明BC⊥面APC,从而证得平面ABC⊥平面APC;
解析试题分析:解:(1)由已知得,MD是△ABP的中位线 ∴MD∥AP
∵MD?面APC,AP?面APC
∴MD∥面APC
(2)∵△PMB为正三角形,D为PB的中点,
∴MD⊥PB,∴AP⊥PB 又∵AP⊥PC,PB∩PC=P ∴AP⊥面PBC
∵BC?面PBC ∴AP⊥BC 又∵BC⊥AC,AC∩AP=A
∴BC⊥面APC ∵BC?面ABC ∴平面ABC⊥平面APC
考点:线面平行和面面垂直
点评:解决的关键是利用线面和面面的平行和垂直的判定定理来分析证明,属于基础题。

练习册系列答案
相关题目
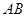 为圆
为圆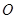 的直径,点
的直径,点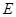 、
、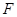 在圆
在圆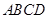 所在的平面和圆
所在的平面和圆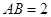 ,
,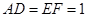 .
.
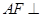 平面
平面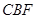 ;
;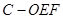 的体积.
的体积.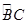 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).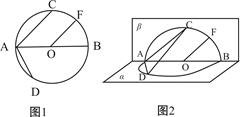
 上是否存在点
上是否存在点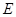 ,使得平面
,使得平面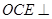 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点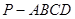 中,
中,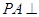 平面
平面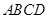 ,底面
,底面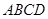 是菱形,
是菱形,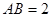 ,
,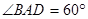 .
.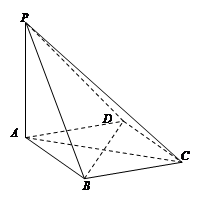
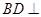
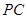 ;
;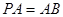 ,求二面角
,求二面角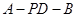 的余弦值.
的余弦值. 中,
中, ,
, ,
, 是角平分线。求证:
是角平分线。求证: 。
。
 中,
中, ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,
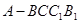 中,
中, 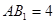 ,底面ABC是正三角形,
,底面ABC是正三角形,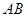 =2.四边形
=2.四边形 是矩形,二面角
是矩形,二面角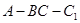 为直二面角,D为
为直二面角,D为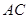 中点。
中点。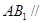 平面
平面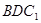 ;
;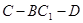 的余弦值.
的余弦值.