题目内容
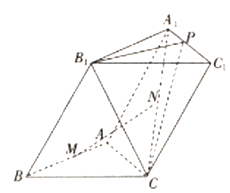
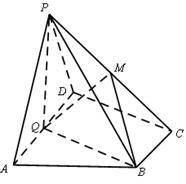
(本小题满分12分)如图,五面体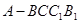 中,
中, 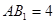 ,底面ABC是正三角形,
,底面ABC是正三角形,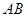 =2.四边形
=2.四边形 是矩形,二面角
是矩形,二面角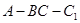 为直二面角,D为
为直二面角,D为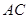 中点。
中点。
(I)证明: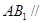 平面
平面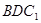 ;
;
(II)求二面角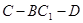 的余弦值.
的余弦值.
(1)根据中位线的性质,做辅助线得到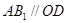 ,然后结合线面平行的判定定理得到结论。
,然后结合线面平行的判定定理得到结论。
(2)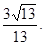
解析试题分析:解:说明:由于建立空间直角坐标系的多样性,所以解法也具有多样性,以下解法仅供参考。
(I)证明:连结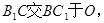 连结
连结 ,
,

∵四边形 是矩形 ∴
是矩形 ∴ 为
为 中点
中点
∵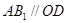

 ∥平面
∥平面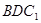 ,
,
(II)建立空间直角坐标系 如图所示,
如图所示,
则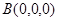 ,
, ,
, ,
, ,
,
所以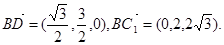
设 为平面
为平面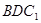 的法向量,
的法向量,
则有 ,
,
即
令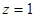 ,可得平面
,可得平面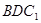 的一个
的一个
法向量为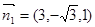 ,
,
而平面 的法向量为
的法向量为 ,
,
所以 ,
,
所以二面角 的余弦值为
的余弦值为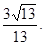
考点:空间中线面的位置关系以及二面角的求解
点评:解决立体几何中的线面的位置关系的判定和二面角的问题,一般可以从两个角度来得到,几何性质法,以及向量法得到,注意灵活的掌握,属于基础题。

练习册系列答案
相关题目
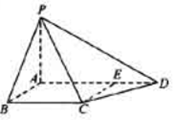
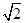 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积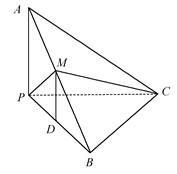
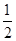 AD=1,CD=
AD=1,CD=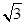 .
.
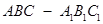 中,△
中,△ 是边长为
是边长为 的等边三角形,
的等边三角形, 平面
平面 ,
, 分别是
分别是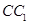 ,
, 的中点.
的中点. 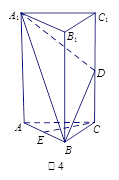
 ∥平面
∥平面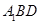 ;
; 为
为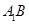 上的动点,当
上的动点,当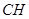 与平面
与平面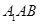 所成最大角的正切值为
所成最大角的正切值为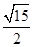 时,
时,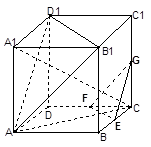
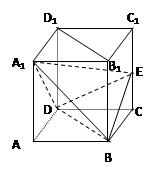
 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形,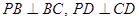 ,且
,且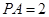 ,
,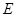 为
为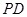 中点.
中点.
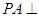 平面
平面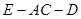 的余弦值.
的余弦值.