题目内容
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
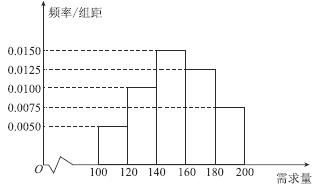
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据频率直方图的数据结合中位数的定义即可求解;(2)根据![]() 的取值范围分类讨论即可求解;(3)首先求得
的取值范围分类讨论即可求解;(3)首先求得![]() 的取值范围,再结合频率直方图即可求解.
的取值范围,再结合频率直方图即可求解.
试题解析:(1)由频率直方图得:需求量为![]() 的频率
的频率![]() ,
,
需求量为![]() 的频率
的频率![]() ,需求量为
,需求量为![]() 的频率
的频率![]() ,
,
则中位数![]() ;(2)∵每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,
;(2)∵每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,∴
,∴![]() ;(3)∵利润不少于4800元,∴
;(3)∵利润不少于4800元,∴![]() ,解得
,解得![]() ,
,
∴由(1)知利润不少于4800元的概率![]() .
.

练习册系列答案
相关题目