题目内容
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
【答案】①②④
【解析】
由三视图还原几何体,可知该几何体为四棱锥,PA⊥底面ABCD,PA=2,底面ABCD为矩形,AB=2,BC=4,然后逐一分析四个命题得答案.
由三视图还原原几何体如图,
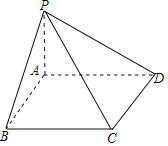
可知该几何体为四棱锥,PA⊥底面ABCD,PA=2,
底面ABCD为矩形,AB=2,BC=4,
则四个侧面是直角三角形,故①正确;
最长棱为PC,长度为2![]() ,故②正确;
,故②正确;
由已知可得,PB=2![]() ,PC=2
,PC=2![]() ,PD=2
,PD=2![]() ,则四个侧面均不全等,故③错误;
,则四个侧面均不全等,故③错误;
把四棱锥补形为长方体,则其外接球半径为![]() PC=
PC=![]() ,其表面积为4π×
,其表面积为4π×![]() =24π,故④正确.
=24π,故④正确.
∴其中正确的命题是①②④.
故答案为:①②④.

【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
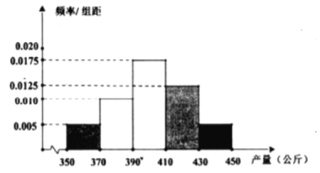
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: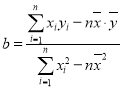 ,
,![]() (回归方程
(回归方程![]() 中)
中)
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与![]() 的浓度是否相关,现采集到某城市周一至周五某时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某时间段车流量与![]() 浓度的数据如下表:
浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 39 | 40 | 42 | 44 | 45 |
(1)根据上表数据,求出这五组数据组成的散点图的样本中心坐标;
(2)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若周六同一时间段车流量是100万辆,试根据(2)求出的线性回归方程预测,此时![]() 的浓度是多少?
的浓度是多少?
(参考公式: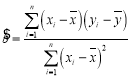 ,
,![]() )
)
【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中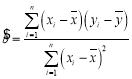
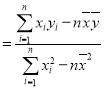 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)