题目内容
17.已知向量$\overrightarrow{m}$=(2$\sqrt{3}$sinx,cosx),$\overrightarrow{n}$=(cosx,2cosx),设函数f(x)=$\overrightarrow{m}•\overrightarrow{n}$.(1)求f(x)的单调递增区间;
(2)设△ABC三个内角A,B,C所对的边分别为a,b,c,f(B)=2且a+c=3,△ABC的面积S=$\frac{\sqrt{3}}{2}$,求b的值.
分析 (1)根据平面向量的数量积,利用三角函数的恒等变换以及三角函数的图象与性质,即可求出f(x)的单调增区间;
(2)根据题意,求出角B的值,利用三角形的面积公式以及余弦定理,求出b的值.
解答 解:(1)∵向量$\overrightarrow{m}$=(2$\sqrt{3}$sinx,cosx),$\overrightarrow{n}$=(cosx,2cosx),
∴f(x)=$\overrightarrow{m}•\overrightarrow{n}$=2$\sqrt{3}$sinxcosx+2cos2x
=$\sqrt{3}$sin2x+(cos2x+1)
=2(sin2xcos$\frac{π}{6}$+cos2xsin$\frac{π}{6}$)+1
=2sin(2x+$\frac{π}{6}$)+1;
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{2π}{3}$+2kπ≤2x≤$\frac{π}{3}$+2kπ,k∈Z,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
∴函数f(x)的单调增区间是[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z;
(2)在△ABC中,f(B)=2,
即2sin(2B+$\frac{π}{6}$)+1=2,
∴sin(2B+$\frac{π}{6}$)=$\frac{1}{2}$,
∴2B+$\frac{π}{6}$=$\frac{5π}{6}$,
解得B=$\frac{π}{3}$;
∴△ABC的面积为S=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴ac=2;
又a+c=3,
∴由余弦定理得
b2=a2+c2-2accosB=a2+c2-ac=(a+c)2-3ac=32-3×2=3,
∴b=$\sqrt{3}$.
点评 本题考查了平面向量数量积的坐标运算问题,也考查了三角函数的图象与性质的应用问题,考查了正弦和余弦定理的应用问题,是综合性题目.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 不等边三角形 | B. | 三条边不全相等的三角形 | ||
| C. | 锐角三角形 | D. | 钝角三角形 |
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于y=x对称 |
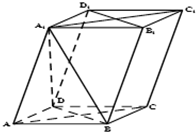 如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.