题目内容
若数列{An}满足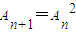 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.(Ⅰ)证明数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;
(Ⅱ)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项及Tn关于n的表达式;
(Ⅲ)记
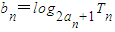 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
【答案】分析:(I)利用点(an,an+1)在函数f(x)=2x2+2x的图象,结合新定义,可得数列{2an+1}是“平方递推数列”,两边取对数,即可证得数列{lg(2an+1)}为首项是lg5公比为2的等比数列;
(II)由题意,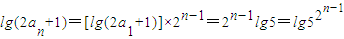 ,从而可得数列{an}的通项,进而先求对数的和,即可求得结论;
,从而可得数列{an}的通项,进而先求对数的和,即可求得结论;
(III)确定数列{bn}的通项,利用等比数列的求和公式可结论.
解答:(I)证明:因为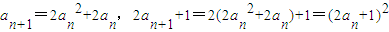
所以数列{2an+1}是“平方递推数列”.--------(2分)
由以上结论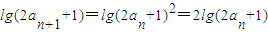 ,
,
所以数列{lg(2an+1)}为首项是lg5公比为2的等比数列.--------(4分)
(II)解:由题意,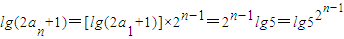 ,
,
∴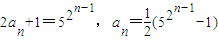 .--------(6分)
.--------(6分)
∴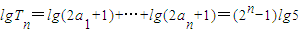 ,
,
∴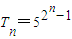 .--------(9分)
.--------(9分)
(III)解: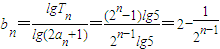 ,
,
∴数列{bn}的前n项和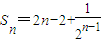 .--------(13分)
.--------(13分)
[注:若有其它解法,请酌情给分]
点评:本题考查新定义,考查数列的通项与求和,解题的关键是正确理解新定义,属于中档题.
(II)由题意,
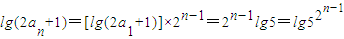 ,从而可得数列{an}的通项,进而先求对数的和,即可求得结论;
,从而可得数列{an}的通项,进而先求对数的和,即可求得结论;(III)确定数列{bn}的通项,利用等比数列的求和公式可结论.
解答:(I)证明:因为
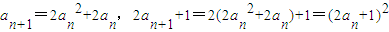
所以数列{2an+1}是“平方递推数列”.--------(2分)
由以上结论
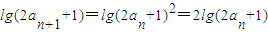 ,
,所以数列{lg(2an+1)}为首项是lg5公比为2的等比数列.--------(4分)
(II)解:由题意,
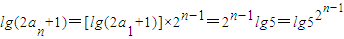 ,
,∴
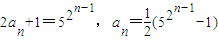 .--------(6分)
.--------(6分)∴
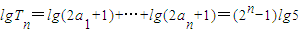 ,
,∴
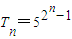 .--------(9分)
.--------(9分)(III)解:
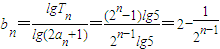 ,
,∴数列{bn}的前n项和
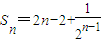 .--------(13分)
.--------(13分)[注:若有其它解法,请酌情给分]
点评:本题考查新定义,考查数列的通项与求和,解题的关键是正确理解新定义,属于中档题.

练习册系列答案
相关题目