题目内容
10.某班同学利用暑假在A、B两个小区逐户进行了一次生活习惯是否符合低碳观念的调查及宣传活动.若生活习惯符合低碳观念的称为“低碳族”,否则,称为“非低碳族”.各小区中,这两“族”人数分别与本小区总人数的比值如下表:| 低碳族 | 非低碳族 | |
| 比值(A小区) | $\frac{1}{2}$ | $\frac{1}{2}$ |
| 比值(B小区) | $\frac{4}{5}$ | $\frac{1}{5}$ |
(Ⅱ)经过大力宣传后的连续两周,A小区“非低碳族”中,每周有20%的人加入到“低碳族”的行列.这两周后,如果从A小区中随机地选出25个人,用ξ表示这25个人中的“低碳族”人数,求数学期望E(ξ).
分析 (Ⅰ)这4人中恰好有两人是低碳族分三类:甲、乙低碳族,丙、丁非低碳族;甲、乙非低碳族,丙、丁低碳族;甲、乙中一人低碳族,一人非低碳族,丙、丁一人低碳族,一人非低碳族;每类中按独立事件求概率,再求和即可.
(Ⅱ)首先求出两周后随机地从A小区中非低碳族的概率,ξ服从二项分布,利用二项分布的期望和方差公式求解即可.
解答 解:(Ⅰ)记“这4人中恰有2人为低碳族”为事件A,则P(A)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{5}×\frac{1}{5}$+4×$\frac{1}{2}×\frac{1}{2}×\frac{4}{5}×\frac{1}{5}$+$\frac{1}{2}×\frac{1}{2}×\frac{4}{5}×\frac{4}{5}$=$\frac{33}{100}$;
(Ⅱ)设A小区的总人数为 a,过两周后,A小区中的“非低碳族”人数与本小区总人数的比为$\frac{a×\frac{1}{2}×(1-\frac{1}{5})^{2}}{a}$=$\frac{8}{25}$
2周后低碳族的概率小区中的“非低碳族”人数与本小区总人数的比为P=1-$\frac{8}{25}$=$\frac{17}{25}$.
依题意ξ~B(25,$\frac{17}{25}$),所以E(ξ)=25×$\frac{17}{25}$=17.
点评 本题考查独立事件、互斥事件的概率及二项分布的期望知识,考查分析问题、解决问题的能力.

练习册系列答案
相关题目
10.下列等式不成立的是( )
| A. | log34=$\frac{lg4}{lg3}$ | B. | log34=$\frac{ln4}{ln3}$ | ||
| C. | log34=$\frac{1}{lo{g}_{4}3}$ | D. | log34=$\frac{lo{g}_{1}4}{lo{g}_{1}3}$ |
5.执行如图所示的程序框图,则输出k的值为( )
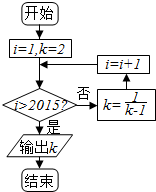

| A. | -1 | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
15.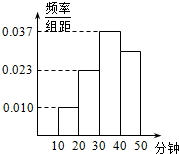 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )| A. | 180 | B. | 450 | C. | 360 | D. | 270 |
2.已知m为实数,且sinα,cosα是关于x的方程3x2-mx+1=0的两根,则sin4α+cos4α的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
19.在如图的程序框图中,若输入的值为2,则输出的值为( )
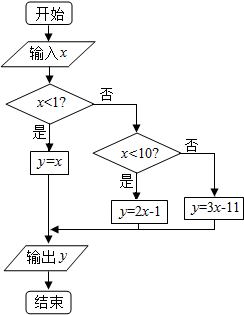

| A. | 2 | B. | 3 | C. | -5 | D. | 6 |