题目内容
12.已知函数f(x)=$\frac{1}{2}$x2+alnx.(1)若a=1,求f(x)在点(1,f(1))处的切线方程;
(2)若a=-2,求函数f(x)在[1,e]上的最大值和最小值.
分析 (1)a=1时,求出f(x)=$\frac{1}{2}{x}^{2}+lnx$,然后求导数f′(x),从而可求出切线的斜率为f′(1),f(1)可以求出,根据直线的点斜式方程即可得出切线方程;
(2)a=-2时,求出f(x)=$\frac{1}{2}{x}^{2}-2lnx$,求导数f′(x)=$\frac{{x}^{2}-2}{x}$,从而可以判断f′(x)在[1,e]上的符号,再根据端点值便可得出f(x)在[1,e]上的最大值和最小值.
解答 解:(1)a=1时,$f(x)=\frac{1}{2}{x}^{2}+lnx$,$f′(x)=x+\frac{1}{x}$;
∴f′(1)=2,f(1)=$\frac{1}{2}$;
即切线的斜率为2,过点(1,$\frac{1}{2}$);
∴切线方程为:$y-\frac{1}{2}=2(x-1)$;
即y=$2x-\frac{3}{2}$;
(2)a=-2时,$f(x)=\frac{1}{2}{x}^{2}-2lnx$,$f′(x)=x-\frac{2}{x}=\frac{{x}^{2}-2}{x}$;
∴$x∈[1,\sqrt{2})$时,f′(x)<0,x$∈(\sqrt{2},e]$时,f′(x)>0;
∴$x=\sqrt{2}$时,f(x)取最小值1-ln2,又f(1)=$\frac{1}{2}$,f(e)=$\frac{1}{2}{e}^{2}-2$>$\frac{1}{2}$;
∴f(x)的最大值为$\frac{1}{2}{e}^{2}-2$.
点评 考查过函数上某点的切线的斜率和该函数在切点处导数的关系,直线的点斜式方程,根据导数求函数在闭区间上最大、最小值的方法:根据导数符号求极值,再比较端点值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.f(x)=log${\;}_{\frac{1}{2}}$${\;}^{3{x}^{2}-ax+5}$在[-1,+∞)单调递减,则a的取值范围为( )
| A. | (-∞,-6] | B. | (-8,-6] | C. | (-8,-6) | D. | [-6,+∞) |
7.已知函数f(x)=|log4x|,正实数m、n满足m<n,且f(m)=2f(n),若f(x)在区间[m2,n]上的最大值为2,则m+n=( )
| A. | $\frac{9}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$或$\frac{3}{4}$ | D. | $\frac{5}{2}$或$\frac{3}{4}$ |
4.抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1,x2,直线与x轴交点的横坐标是x3,则恒有( )
| A. | x3=x1+x2 | B. | x1x2=x1x3+x2x3 | ||
| C. | x1+x2+x3=0 | D. | x1x2+x2x3+x3x1=0 |
1.动圆M经过点A(3,0)且与直线l:x=-3相切,则动圆圆心M的轨迹方程是( )
| A. | y2=12x | B. | y2=6x | C. | y2=3x | D. | y2=24x |
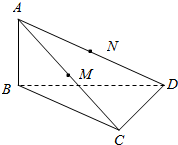 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.