题目内容
已知y=f(x)(x∈D,D为此函数的定义域)同时满足下列两个条件:①函数f(x)在D内单调递增或单调递减;②如果存在区间[a,b]⊆D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数.请解答以下问题:
(1)判断函数f(x)=1+x-x2(x∈(0,+∞))是否为闭函数?并说明理由;
(2)求证:函数y=-x3(x∈[-1,1])为闭函数;
(3)若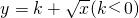 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
解:(1)函数f(x)在区间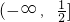 上单调递减,在
上单调递减,在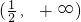 上单调递增;
上单调递增;
所以,函数在定义域上不是单调递增或单调递减函数,从而该函数不是闭函数.
(2)先证y=-x3符合条件①:对于任意x1,x2∈[-1,1],且x1<x2,
有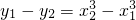 =
=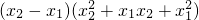 =
=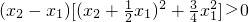 ,
,
∴y1>y2,故y=-x3是R上的减函数.
又因为y=-x3在[-1,1]上的值域是[-1,1].
所以函数y=-x3(x∈[-1,1])为闭函数;
(3)易知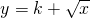 是(0,+∞)上的增函数,符合条件①;
是(0,+∞)上的增函数,符合条件①;
设函数符合条件②的区间为[a,b],则有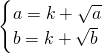 ;
;
故a,b是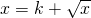 的两个不等根,即方程组为:
的两个不等根,即方程组为: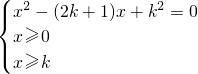 有两个不等非负实根;
有两个不等非负实根;
设x1,x2为方程x2-(2k+1)x+k2=0的二根,则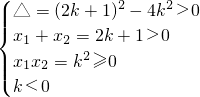 ,
,
解得: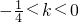
∴k的取值范围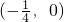 .
.
分析:(1)可判断函数f(x)在定义域内不单调,由闭函数的定义可作出判断;
(2)按照闭函数的定义只需证明两条:①在定义域内单调;②该函数值域也为[-1,1];
(3)由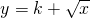 是(0,+∞)上的增函数,知其符合条件①;
是(0,+∞)上的增函数,知其符合条件①;
设函数符合条件②的区间为[a,b],从而有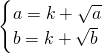 ,问题转化为方程
,问题转化为方程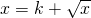 有两个不等非负实根,利用二次方程根的分布知识可得k的限制条件;
有两个不等非负实根,利用二次方程根的分布知识可得k的限制条件;
点评:本题考查新定义,考查导数知识的运用,解题的关键是理解新定义,并利用新定义求参数的值.
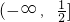 上单调递减,在
上单调递减,在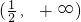 上单调递增;
上单调递增;所以,函数在定义域上不是单调递增或单调递减函数,从而该函数不是闭函数.
(2)先证y=-x3符合条件①:对于任意x1,x2∈[-1,1],且x1<x2,
有
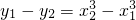 =
=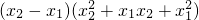 =
=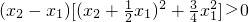 ,
,∴y1>y2,故y=-x3是R上的减函数.
又因为y=-x3在[-1,1]上的值域是[-1,1].
所以函数y=-x3(x∈[-1,1])为闭函数;
(3)易知
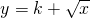 是(0,+∞)上的增函数,符合条件①;
是(0,+∞)上的增函数,符合条件①;设函数符合条件②的区间为[a,b],则有
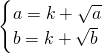 ;
;故a,b是
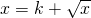 的两个不等根,即方程组为:
的两个不等根,即方程组为: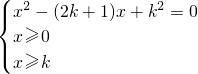 有两个不等非负实根;
有两个不等非负实根;设x1,x2为方程x2-(2k+1)x+k2=0的二根,则
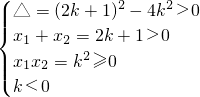 ,
,解得:
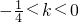
∴k的取值范围
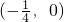 .
.分析:(1)可判断函数f(x)在定义域内不单调,由闭函数的定义可作出判断;
(2)按照闭函数的定义只需证明两条:①在定义域内单调;②该函数值域也为[-1,1];
(3)由
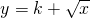 是(0,+∞)上的增函数,知其符合条件①;
是(0,+∞)上的增函数,知其符合条件①;设函数符合条件②的区间为[a,b],从而有
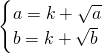 ,问题转化为方程
,问题转化为方程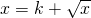 有两个不等非负实根,利用二次方程根的分布知识可得k的限制条件;
有两个不等非负实根,利用二次方程根的分布知识可得k的限制条件;点评:本题考查新定义,考查导数知识的运用,解题的关键是理解新定义,并利用新定义求参数的值.

练习册系列答案
相关题目
 是函数y=g(x) 图象上的点.
是函数y=g(x) 图象上的点. 上存在两个不同点关于直线y=x对称,求出其坐标;若曲线
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围; 及
及 加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)