题目内容
已知函数f(x)=log2(x+1),当点 (x,y) 是函数y=f (x) 图象上的点时,点 是函数y=g(x) 图象上的点.
是函数y=g(x) 图象上的点.(1)写出函数y=g (x) 的表达式;
(2)当g(x)-f (x)≥0时,求x的取值范围;
(3)当x在 (2)所给范围内取值时,求g(x)-f(x)的最大值.
【答案】分析:(1)令 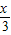 =X,
=X,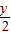 =Y,由题设条件知 Y=
=Y,由题设条件知 Y= log2(3X+1),再由(X,Y)是函数y=g(x)的图象上的点,即可得到函数y=g(x)的解析式.
log2(3X+1),再由(X,Y)是函数y=g(x)的图象上的点,即可得到函数y=g(x)的解析式.
(2)由题意知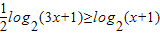 .由对数函数的性质可得
.由对数函数的性质可得 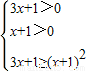 ,解不等式组即可得到使g(x)>f(x)的x的取值范围.
,解不等式组即可得到使g(x)>f(x)的x的取值范围.
(3)由题设条件知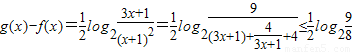 .由此可知结合基本不等式即可求出g(x)-f(x)在[0,1]上的最大值.
.由此可知结合基本不等式即可求出g(x)-f(x)在[0,1]上的最大值.
解答:解:(1)令X= ,Y=
,Y=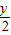 ,
,
∴x=3X,y=2Y,
∵点 (x,y) 是函数y=f (x) 图象上,
∴2Y=log2(3X+1),
即Y= log2(3X+1),
log2(3X+1),
∴g (x)= log2(3x+1)(x>-
log2(3x+1)(x>- );
);
(2)由g(x)-f (x)≥0,得 log2(3x+1)-log2(x+1)≥0,
log2(3x+1)-log2(x+1)≥0,
∴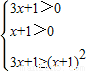 ,
,
解得0≤x≤1;
∴x的取值范围为0≤x≤1;
(3)∵因为0≤x≤1,
所以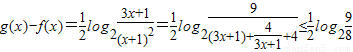 .
.
当且仅当3x+1=2时,即 x= 时等号成立,
时等号成立,
故g(x)-f(x)在[0,1]上的最大值为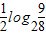 =log23-
=log23- .
.
点评:本题考查的知识点是对数函数的图象与性质的综合应用,其中(1)中求解析式是坐标法中的“点随点动”问题,(2)中关键是根据对数函数的性质构造关于x的不等式组,(3)的关键是根据基本不等式,求出真数部分的最大值,进而根据对数函数的单调性,得到y=g(x)-f(x)的最大值.
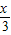 =X,
=X,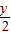 =Y,由题设条件知 Y=
=Y,由题设条件知 Y= log2(3X+1),再由(X,Y)是函数y=g(x)的图象上的点,即可得到函数y=g(x)的解析式.
log2(3X+1),再由(X,Y)是函数y=g(x)的图象上的点,即可得到函数y=g(x)的解析式.(2)由题意知
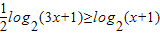 .由对数函数的性质可得
.由对数函数的性质可得 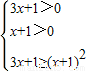 ,解不等式组即可得到使g(x)>f(x)的x的取值范围.
,解不等式组即可得到使g(x)>f(x)的x的取值范围.(3)由题设条件知
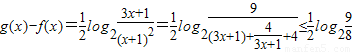 .由此可知结合基本不等式即可求出g(x)-f(x)在[0,1]上的最大值.
.由此可知结合基本不等式即可求出g(x)-f(x)在[0,1]上的最大值.解答:解:(1)令X=
 ,Y=
,Y=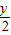 ,
,∴x=3X,y=2Y,
∵点 (x,y) 是函数y=f (x) 图象上,
∴2Y=log2(3X+1),
即Y=
 log2(3X+1),
log2(3X+1),∴g (x)=
 log2(3x+1)(x>-
log2(3x+1)(x>- );
);(2)由g(x)-f (x)≥0,得
 log2(3x+1)-log2(x+1)≥0,
log2(3x+1)-log2(x+1)≥0,∴
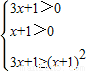 ,
,解得0≤x≤1;
∴x的取值范围为0≤x≤1;
(3)∵因为0≤x≤1,
所以
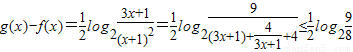 .
.当且仅当3x+1=2时,即 x=
 时等号成立,
时等号成立,故g(x)-f(x)在[0,1]上的最大值为
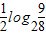 =log23-
=log23- .
.点评:本题考查的知识点是对数函数的图象与性质的综合应用,其中(1)中求解析式是坐标法中的“点随点动”问题,(2)中关键是根据对数函数的性质构造关于x的不等式组,(3)的关键是根据基本不等式,求出真数部分的最大值,进而根据对数函数的单调性,得到y=g(x)-f(x)的最大值.

练习册系列答案
相关题目