题目内容
已知y=f(x)是定义域为(
,+∞)的可导函数,f(1)=f(3)=1,f(x)的导数为f′(x),且x∈(
,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0,则不等式组
所表示的平面区域的面积等于( )
| 1 |
| 2 |
| 1 |
| 2 |
|
分析:此题关键是找出可行域,已知y=f(x)是定义域为(
,+∞)的可导函数,f(1)=f(3)=1,f(x)的导数为f′(x),且x∈(
,2)时,f′(x)<0;x∈(2,+∞),说明f(x)在x=2处取得极小值,若f(2x+y)≤1,可得1≤2x+y≤3,画出可行域,根据线性规划问题进行求解;
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵y=f(x)是定义域为(
,+∞)的可导函数,f(1)=f(3)=1,f(x)的导数为f′(x),且x∈(
,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0,
说明f(x)在(
,2)为减函数,在(2,+∞)为增函数,在x=2取得极小值,
因为f(1)=f(3)=1,要使f(2x+y)≤1,可得1≤2x+y≤3①,
结合-2≤x-2y≤
②画出满足条件①②的可行域可得:
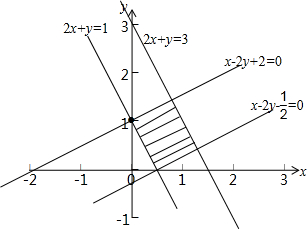
可知直线x-2y+2=0与2x+y=1、2x+y=3垂直,
所表示的平面区域是一个长方形,边长等于点(0,1)到直线2x+y=3的距离:d=
=
,
另一条边等于:
=
所以面积S=
×
=1,
故选D;
| 1 |
| 2 |
| 1 |
| 2 |
说明f(x)在(
| 1 |
| 2 |
因为f(1)=f(3)=1,要使f(2x+y)≤1,可得1≤2x+y≤3①,
结合-2≤x-2y≤
| 1 |
| 2 |

可知直线x-2y+2=0与2x+y=1、2x+y=3垂直,
所表示的平面区域是一个长方形,边长等于点(0,1)到直线2x+y=3的距离:d=
| |1-3| | ||
|
| 2 | ||
|
另一条边等于:
1+
|
| ||
| 2 |
所以面积S=
| 2 | ||
|
| ||
| 2 |
故选D;
点评:此题是一道线性规划问题,利用导数研究函数的单调性,找出可行域,是解决此题的关键,此题是一道好题!

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+ 已知函数f(x)=2x+
已知函数f(x)=2x+