题目内容
设定义在R上的函数f(x)=ax4+a1x3+a2x2+a3x+a4,a,a1,a2,a3,a4∈R,当x=-1时,f(x)取得极大值 ,且函数y=f(x+1)的图象关于点(-1,0)对称.
,且函数y=f(x+1)的图象关于点(-1,0)对称.(Ⅰ)求f(x)的表达式;
(Ⅱ)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
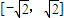 上?如果存在,求出点的坐标;如果不存在,请说明理由;
上?如果存在,求出点的坐标;如果不存在,请说明理由;(Ⅲ)设
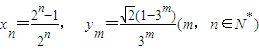 ,求证:
,求证: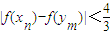 .
.
【答案】分析:(Ⅰ)已知函数f(x),且函数y=f(x+1)的图象关于点(-1,0)对称.所以y=f(x)的图象关于点(0,0)对称,即y=f(x)是奇函数,所以f(x)=a1x3+a3x,由题意,得 进而可得答案;
进而可得答案;
(Ⅱ)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在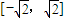 上?属于探索性问题.通常假设存在,看是否有解即可.假设存在两切点为
上?属于探索性问题.通常假设存在,看是否有解即可.假设存在两切点为 ,
,
则f'(x1)•f'(x2)=(x12-1)(x22-1)=-1.因为(x12-1)、(x22-1)∈[-1,1]
所以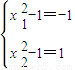 或
或 即
即 或
或
从而可得所求两点的坐标分别为 或
或 .
.
(Ⅲ)设 ,求证:
,求证: .关键在理解题意上.只需要求出
.关键在理解题意上.只需要求出
 和
和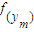 的最值即可.求最值当然要通过求导分析单调性,再看
的最值即可.求最值当然要通过求导分析单调性,再看 ,所属范围.再求.则易证
,所属范围.再求.则易证 .
.
解答:解:(Ⅰ)将y=f(x+1)的图象向右平移1个单位,得到y=f(x)的图象,
所以y=f(x)的图象关于点(0,0)对称,即y=f(x)是奇函数,
所以f(x)=a1x3+a3x,由题意,得 所以
所以 .
.
(Ⅱ)由(Ⅰ)得f'(x)=x2-1,
假设存在两切点为 ,
,
则f'(x1)•f'(x2)=(x12-1)(x22-1)=-1.因为(x12-1)、(x22-1)∈[-1,1]
所以 或
或 即
即 或
或
从而可得所求两点的坐标分别为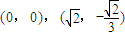 或
或 .
.
(Ⅲ)因为当 时,f'(x)<0,所以f(x)在
时,f'(x)<0,所以f(x)在 递减.
递减.
由已知得 ,
,
所以 ,即
,即 .
.
注意到x<-1时,f′(x)>0,-1<x<1时,f′(x)<0,
故f(x)在(-∞,-1)上递增,在(-1,1)上递减,
由于ym= ,
,
所以 .
.
因为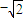 <-1<
<-1< ,
,
所以 ,
,
即 .
.
所以 .
.
点评:这种题型属于较难的压轴题.关键在挖掘题意上做文章.
 进而可得答案;
进而可得答案;(Ⅱ)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
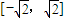 上?属于探索性问题.通常假设存在,看是否有解即可.假设存在两切点为
上?属于探索性问题.通常假设存在,看是否有解即可.假设存在两切点为 ,
,则f'(x1)•f'(x2)=(x12-1)(x22-1)=-1.因为(x12-1)、(x22-1)∈[-1,1]
所以
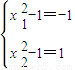 或
或 即
即 或
或
从而可得所求两点的坐标分别为
 或
或 .
.(Ⅲ)设
 ,求证:
,求证: .关键在理解题意上.只需要求出
.关键在理解题意上.只需要求出 和
和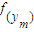 的最值即可.求最值当然要通过求导分析单调性,再看
的最值即可.求最值当然要通过求导分析单调性,再看 ,所属范围.再求.则易证
,所属范围.再求.则易证 .
.解答:解:(Ⅰ)将y=f(x+1)的图象向右平移1个单位,得到y=f(x)的图象,
所以y=f(x)的图象关于点(0,0)对称,即y=f(x)是奇函数,
所以f(x)=a1x3+a3x,由题意,得
 所以
所以 .
.(Ⅱ)由(Ⅰ)得f'(x)=x2-1,
假设存在两切点为
 ,
,则f'(x1)•f'(x2)=(x12-1)(x22-1)=-1.因为(x12-1)、(x22-1)∈[-1,1]
所以
 或
或 即
即 或
或
从而可得所求两点的坐标分别为
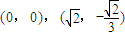 或
或 .
.(Ⅲ)因为当
 时,f'(x)<0,所以f(x)在
时,f'(x)<0,所以f(x)在 递减.
递减.由已知得
 ,
,所以
 ,即
,即 .
.注意到x<-1时,f′(x)>0,-1<x<1时,f′(x)<0,
故f(x)在(-∞,-1)上递增,在(-1,1)上递减,
由于ym=
 ,
,所以
 .
.因为
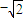 <-1<
<-1< ,
,所以
 ,
,即
 .
.所以
 .
.点评:这种题型属于较难的压轴题.关键在挖掘题意上做文章.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |