Question

【题目】设f(x)是定义域为R的周期函数，最小正周期为2，且f(1＋x)＝f(1－x)，当－1≤x≤0时，f(x)＝－x.
（1）判断f(x)的奇偶性；
（2）试求出函数f(x)在区间[－1，2]上的表达式.

Answer 1

【答案】
（1）解：∵f(1＋x)＝f(1－x)，∴f(－x)＝f(2＋x).
又f(x＋2)＝f(x)，∴f(－x)＝f(x).
又f(x)的定义域为R，
∴f(x)是偶函数
（2）解：当x∈[0，1]时，－x∈[－1，0]，
则f(x)＝f(－x)＝x；
进而当1≤x≤2时，－1≤x－2≤0，
f(x)＝f(x－2)＝－(x－2)＝－x＋2.
故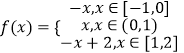
【解析】本题主要考查函数的奇偶性和函数解析式的求法。（1）主要根据定义来判断抽象函数是偶函数。（2）求某个区间的表达式，要根据周期性转化到已知区间上进行求解。