题目内容
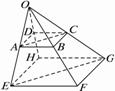
 如右图所示,已知△OAB中,点C是以A为中心的点B的对称点,D在OB上,且
如右图所示,已知△OAB中,点C是以A为中心的点B的对称点,D在OB上,且| OD |
| DB |
| OA |
| a |
| OB |
| b |
(1)用
| a |
| b |
| OC |
| DC |
(2)若
| OE |
| OA |
分析:(1)由
=
(
+
)可求出
,根据
=
-
可求得结果;
(2)由于D、E、C三点共线,可得
=2λ
-
,再由
=-
+μ
,可得λ,μ的方程组,解之即可.
| OA |
| 1 |
| 2 |
| OB |
| OC |
| OC |
| DC |
| OC |
| OD |
(2)由于D、E、C三点共线,可得
| DE |
| a |
| 5 |
| 3 |
| λb |
| DE |
| 2 |
| 3 |
| b |
| a |
解答:解:(1)由题意可得A是BC的中点,所以
=
(
+
),
∴
=2
-
=2
-
,
∴
=
-
=2
-
-
=2
-
,
(2)由于D、E、C三点共线,∴
=λ
=2λ
-
,
又
=
+
=-
+μ
=-
+μ
,
∴2λ
-
=-
+μ
,故有2λ=μ,-
λ=-
,
解得λ=
,μ=
,故实数λ的值为
| OA |
| 1 |
| 2 |
| OB |
| OC |
∴
| OC |
| OA |
| OB |
| a |
| b |
∴
| DC |
| OC |
| OD |
| a |
| b |
| 2 |
| 3 |
| b |
| a |
| 5 |
| 3 |
| b |
(2)由于D、E、C三点共线,∴
| DE |
| DC |
| a |
| 5 |
| 3 |
| λb |
又
| DE |
| DO |
| OE |
| 2 |
| 3 |
| OB |
| OA |
| 2 |
| 3 |
| b |
| a |
∴2λ
| a |
| 5 |
| 3 |
| λb |
| 2 |
| 3 |
| b |
| a |
| 5 |
| 3 |
| 2 |
| 3 |
解得λ=
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
点评:本题考查平面向量基本定理及向量的表示,两个向量共线的性质,两个向量坐标形式的运算,属中档题.

练习册系列答案
相关题目
 双曲线方程为
双曲线方程为 如图所示,已知椭圆M:
如图所示,已知椭圆M: 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 (2012•孝感模拟)在两道题中选择其中一道题作答,若两道都选,按前一道作答结果计分.
(2012•孝感模拟)在两道题中选择其中一道题作答,若两道都选,按前一道作答结果计分.