Question

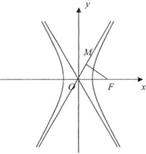双曲线方程为

x2

a2

-

y2

b2

=1(a＞0，b＞0)，过右焦点F向一条渐近线做垂线，垂足为M，如图所示，已知∠MFO=30°（O为坐标原点），则其离心率为（　　）

• A、

  2

• B、

  3

• C、

  2 3

  3

• D、2

Answer 1

分析：根据双曲线方程可知渐近线方程，根据点到直线的距离求得|MF|，根据∠MFO=30°可知|OF|=2|MF|，根据|OF|=c代入，即可求得a和c的关系，离心率可得．

解答：解：依题意可知，其中一个渐近线的方程y=

b

a

x，
|OF|=c=

a2+b2

，F（

a2+b2

，0）

|MF|=

|a a2+b2 |

a2+b2

=a
∵∠MFO=30°
∴|OF|=2|MF|，即c=2a
∴e=

c

a

=2
故选D

点评：本题主要考查了双曲线的简单性质．解此题的关键是从边的关系中找到a和c的关系．