题目内容
（2012•孝感模拟）在两道题中选择其中一道题作答，若两道都选，按前一道作答结果计分．（1）（几何证明选讲题）如右图所示AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是
| 48 |
| 5 |
| 48 |
| 5 |
（2）（坐标系与参数方程题）已知圆的极坐标方程为ρ=2COSθ，则该圆的圆心到直线ρsinθ+2ρcosθ=1的距离是
| ||
| 5 |
| ||
| 5 |
分析：（1）利用勾股定理求出AO，可得AD的值，由直角三角形相似得
=
，求出h 值，代入△ABD的面积公式进行运算．
（2）先利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，将极坐标方程为ρ=2cosθ和ρsinθ+2ρcosθ=1化成直角坐标方程，最后利用直角坐标方程的形式，结合点到直线的距离公式求解即得．
| OB |
| h |
| AO |
| AD |
（2）先利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，将极坐标方程为ρ=2cosθ和ρsinθ+2ρcosθ=1化成直角坐标方程，最后利用直角坐标方程的形式，结合点到直线的距离公式求解即得．
解答：解：（1）由题意得 AO=
=
=5，AD=5+3=8，设D到AB的距离等于h，
由直角三角形相似得
=
=
，h=
．
故△ABD的面积等于
AB•h=
，
故答案为：
．
（2）：由ρ=2cosθ，化为直角坐标方程为x2+y2-2x=0，其圆心是A（1，0），
由ρsinθ+2ρcosθ=1得：
化为直角坐标方程为2x+y-1=0，
由点到直线的距离公式，得d=
=
．
故答案为
．
| AB2+OB2 |
| 16+9 |
由直角三角形相似得
| OB |
| h |
| AO |
| AD |
| 5 |
| 8 |
| 24 |
| 5 |
故△ABD的面积等于
| 1 |
| 2 |
| 48 |
| 5 |
故答案为：
| 48 |
| 5 |
（2）：由ρ=2cosθ，化为直角坐标方程为x2+y2-2x=0，其圆心是A（1，0），
由ρsinθ+2ρcosθ=1得：
化为直角坐标方程为2x+y-1=0，
由点到直线的距离公式，得d=
| |2+0-1| | ||
|
| ||
| 5 |
故答案为
| ||
| 5 |
点评：（1）本题考查直线和圆相切的性质，相似三角形的性质，求出D到AB的距离等于h是解题的关键．
（2）本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化，以及利用圆的几何性质计算圆心到直线的距等基本方法，属于基础题．
（2）本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化，以及利用圆的几何性质计算圆心到直线的距等基本方法，属于基础题．
练习册系列答案
相关题目
（2012•孝感模拟）如图，在A、B间有四个焊接点，若焊接点脱落，而可能导致电路不通，如今发现A、B之间线路不通，则焊接点脱落的不同情况有（ ）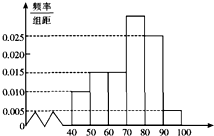
（2012•孝感模拟）某校高一（2）班共有60名同学参加期末考试，现将其数学学科成绩（均为整数）分成六个分数段[40，50），[50，60），…，[90，100]，画出如右图所示的部分频率分布直方图，请观察图形信息，回答下列问题：