题目内容
 如图所示,已知椭圆M:
如图所示,已知椭圆M:| y2 |
| a2 |
| x2 |
| b2 |
| 12 |
| 5 |
(1)求椭圆M的方程;
(2)试判断直线l与x轴是否交于定点?若是,求出定点的坐标;若不是,请说明理由.
分析:(1)由截距式可得直线AB的方程,由点O到直线AB的距离为
可得
=
①,由四个顶点构成菱形可得a2+b2=25②,联立①②解得a,b;
(2)设C(x1,y1)D(x2,y2),将x=my+n代入椭圆方程消掉x可得y的二次方程,由于以CD为直径的圆过椭圆的右顶点P,则可得
•
=0,根据向量数量积运算及韦达定理可得m,n的方程,由此可求出n,然后代入直线方程,可求得定点;
| 12 |
| 5 |
| |ab| | ||
|
| 12 |
| 5 |
(2)设C(x1,y1)D(x2,y2),将x=my+n代入椭圆方程消掉x可得y的二次方程,由于以CD为直径的圆过椭圆的右顶点P,则可得
| PC |
| PD |
解答:解:(1)直线AB的方程为
+
=1,即ax-by+ab=0,
∴原点O到直线AB的距离为
=
①,
由四个顶点构成菱形可得a2+b2=25②,
联立①②解得a=4,b=3,
∴椭圆M的方程为
+
=1;
(2)由(1)知P(3,0),设C(x1,y1)D(x2,y2),
将x=my+n代入椭圆方程,整理得:(9+16m2)y2+32mny+16n2-144=0,
∴y1+y2=-
,y1y2=
,
∴x1x2=(my1+n)(my2+n)=m2y1y2+mn(y1+y2)+n2=m2•
+mn•(-
)+n2=
,
x1+x2=(my1+n)+(my2+n)=m(y1+y2)+2n=-
+2n=
,
∵以CD为直径的圆过椭圆的右顶点P,∴
•
=0,即(x1-3,y1)•(x2-3,y2)=0,
∴y1y2+x1x2-3(x1+x2)+9=0,
∴
+
-3×
+9=0,解得n=3或n=-
,
当n=3时直线x=my+3过P(3,0),此时不合题意;当n=-
时,x=my-
,过定点(-
,0),
故直线l与x轴交于定点(-
,0).
| x |
| -b |
| y |
| a |
∴原点O到直线AB的距离为
| |ab| | ||
|
| 12 |
| 5 |
由四个顶点构成菱形可得a2+b2=25②,
联立①②解得a=4,b=3,
∴椭圆M的方程为
| y2 |
| 16 |
| x2 |
| 9 |
(2)由(1)知P(3,0),设C(x1,y1)D(x2,y2),
将x=my+n代入椭圆方程,整理得:(9+16m2)y2+32mny+16n2-144=0,
∴y1+y2=-
| 32mn |
| 9+16m2 |
| 16n2-144 |
| 9+16m2 |
∴x1x2=(my1+n)(my2+n)=m2y1y2+mn(y1+y2)+n2=m2•
| 16n2-144 |
| 9+16m2 |
| 32mn |
| 9+16m2 |
| 9n2-144m2 |
| 9+16m2 |
x1+x2=(my1+n)+(my2+n)=m(y1+y2)+2n=-
| 32m2n |
| 9+16m2 |
| 18n |
| 9+16m2 |
∵以CD为直径的圆过椭圆的右顶点P,∴
| PC |
| PD |
∴y1y2+x1x2-3(x1+x2)+9=0,
∴
| 16n2-144 |
| 9+16m2 |
| 9n2-144m2 |
| 9+16m2 |
| 18n |
| 9+16m2 |
| 21 |
| 25 |
当n=3时直线x=my+3过P(3,0),此时不合题意;当n=-
| 21 |
| 25 |
| 21 |
| 25 |
| 21 |
| 25 |
故直线l与x轴交于定点(-
| 21 |
| 25 |
点评:本题考查椭圆的标准方程、直线与椭圆的位置关系、向量的数量积运算等知识,考查学生的运算能力,运算量大,能力要求高.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
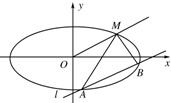 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点. 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 如图所示,已知椭圆C:
如图所示,已知椭圆C: