题目内容
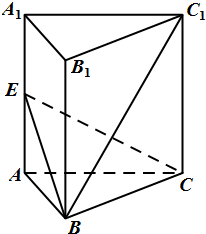 如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.
如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.(Ⅰ)证明:BC1⊥EC;
(Ⅱ)求二面角A-EC-B的大小.
分析:法一:
(Ⅰ)设O是AC的中点,连接OB、OC1.在正三棱柱中,OB⊥AC,OB⊥平面ACC1A1,OC1是BC1在面ACC1A1上的射影.△AEC≌△COC1,由此能够证明BC1⊥EC.
(Ⅱ)由(Ⅰ)知BO⊥平面AEC,作OF⊥EC,垂足为F,连接BF,则∠OFB为二面角A-EC-B的平面角.由此能求出二面角A-EC-B的大小.
法二:
(Ⅰ)在正三棱柱中,以AC的中点O为原点,建立空间直角坐标系,设AB=2,利用向量法能够证明BC1⊥EC.
(Ⅱ)求出平面AEC的一个法向量为
=
.求出平面ECD的法向量
=
.利用向量法能坟出二面角A-EC-B的大小.
(Ⅰ)设O是AC的中点,连接OB、OC1.在正三棱柱中,OB⊥AC,OB⊥平面ACC1A1,OC1是BC1在面ACC1A1上的射影.△AEC≌△COC1,由此能够证明BC1⊥EC.
(Ⅱ)由(Ⅰ)知BO⊥平面AEC,作OF⊥EC,垂足为F,连接BF,则∠OFB为二面角A-EC-B的平面角.由此能求出二面角A-EC-B的大小.
法二:
(Ⅰ)在正三棱柱中,以AC的中点O为原点,建立空间直角坐标系,设AB=2,利用向量法能够证明BC1⊥EC.
(Ⅱ)求出平面AEC的一个法向量为
| n1 |
|
| n2 |
|
解答: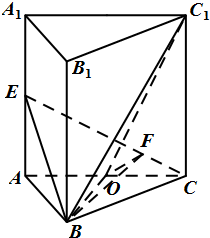 解法一:
解法一:
(Ⅰ)证明:设O是AC的中点,连接OB、OC1.
在正三棱柱中,OB⊥AC,OB⊥平面ACC1A1,
∴OC1是BC1在面ACC1A1上的射影.
∴△AEC≌△COC1,∠AEC=∠COC1.
又∠AEC+∠ACE=90°,
∴∠COC1+∠ACE=90°,OC1⊥EC,
∴BC1⊥EC.…(6分)
(Ⅱ)解:由(Ⅰ)知BO⊥平面AEC,
作OF⊥EC,垂足为F,连接BF,
则∠OFB为二面角A-EC-B的平面角.
不妨设AB=2,则BO=
,OF=
,
在Rt△BOF中,tan∠OFB=
=
,
∴∠OFB=arctan
.…(12分)
解法二:
(Ⅰ)证明:在正三棱柱中,以AC的中点O为原点,建立空间直角坐标系O-xyz如图.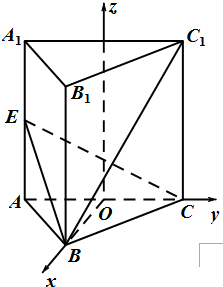
设AB=2,则
B
,C
,C1
,E
,
∴
=
,
=
,
∵
•
=0+2-2=0.
∴BC1⊥EC.…(6分)
(Ⅱ)解:在空间直角坐标系O-xyz中,
平面AEC的一个法向量为
=
.
设平面ECD的法向量为
=
,
易知
=
,1,0),
=
.
由
,得
,
取x=1,得
=
.
cos?
,
>=
=
=
,
∴二面角A-EC-B的大小为arccos
.…(12分)
 解法一:
解法一:(Ⅰ)证明:设O是AC的中点,连接OB、OC1.
在正三棱柱中,OB⊥AC,OB⊥平面ACC1A1,
∴OC1是BC1在面ACC1A1上的射影.
∴△AEC≌△COC1,∠AEC=∠COC1.
又∠AEC+∠ACE=90°,
∴∠COC1+∠ACE=90°,OC1⊥EC,
∴BC1⊥EC.…(6分)
(Ⅱ)解:由(Ⅰ)知BO⊥平面AEC,
作OF⊥EC,垂足为F,连接BF,
则∠OFB为二面角A-EC-B的平面角.
不妨设AB=2,则BO=
| 3 |
| 1 | ||
|
在Rt△BOF中,tan∠OFB=
| OB |
| OF |
| 15 |
∴∠OFB=arctan
| 15 |
解法二:
(Ⅰ)证明:在正三棱柱中,以AC的中点O为原点,建立空间直角坐标系O-xyz如图.

设AB=2,则
B
|
|
|
|
∴
| BC1 |
|
| EC |
|
∵
| BC1 |
| EC |
∴BC1⊥EC.…(6分)
(Ⅱ)解:在空间直角坐标系O-xyz中,
平面AEC的一个法向量为
| n1 |
|
设平面ECD的法向量为
| n2 |
|
易知
| BC |
|
| EC |
|
由
|
|
取x=1,得
| n2 |
|
cos?
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 1×4 |
| 1 |
| 4 |
∴二面角A-EC-B的大小为arccos
| 1 |
| 4 |
点评:本题考查异面直线垂直的证明,考查二面角的求法,解题时要认真审题,合理地化空间问题为平面问题,注意向量法的合理运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.