题目内容
2.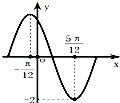 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则此函数的解析式为( )| A. | y=2sin(2x+$\frac{π}{3}$) | B. | y=2sin($\frac{x}{2}$-$\frac{π}{3}$) | C. | y=2sin(2x-$\frac{π}{3}$) | D. | y=2sin(2x+$\frac{2π}{3}$) |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:由函数的最小值为-2可得A=2,再根据$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{5π}{12}$-(-$\frac{π}{12}$)=$\frac{π}{2}$,求得ω=2,
再根据五点法作图可得2×(-$\frac{π}{12}$)+φ=$\frac{π}{2}$,求得φ=$\frac{2π}{3}$,故函数的解析式为y=2sin(2x+$\frac{2π}{3}$),
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各组向量中,可以作为基底的是( )
| A. | $\overrightarrow{{e}_{1}}$=(-1,2),$\overrightarrow{{e}_{2}}$=(5,7) | B. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,-2) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=($\frac{1}{2}$,-$\frac{3}{4}$) |
13.某中学高三年级周六一天有补课.其中上午4节,下午2节.要排语文、数学、英语、物理、化学、生物课各一节,要求上午第一节课不排生物,数学必须排在上午,则不同排法共有( )
| A. | 384种 | B. | 408种 | C. | 480种 | D. | 600种 |
10.已知向量$\overrightarrow a、\overrightarrow b$满足$|\overrightarrow a|=1、|\overrightarrow b|=\sqrt{3}$,且$(3\overrightarrow a-2\overrightarrow b)⊥\overrightarrow a$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
17.下列说法不正确的是( )
| A. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是““?x∈R,x2-x-1≥0” | |
| C. | 当a<0时,幂函数y=xa在(0,+∞)上单调递减 | |
| D. | “φ=$\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 |
14.已知函数f(x)=|sinx|,下列结论中错误的是( )
| A. | f(x)既偶函数,又是周期函数. | B. | f(x)的最大值为$\frac{\sqrt{3}}{2}$ | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)的图象关于直线x=π对称 |
12.学校教务处要从某班级学号为1-60的60名学生中用系统抽样方法抽取6名同学的作业进行检查,则被抽到的学生的学号可能是( )
| A. | 5,10,15,20,25,30 | B. | 3,13,23,33,43,53 | ||
| C. | 1,2,3,4,5,6 | D. | 2,4,8,16,32,48 |