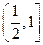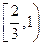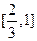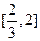题目内容
已知函数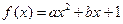 (
(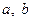 为实数,
为实数,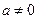 ,
,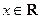 ),
),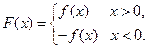
(1)若 ,且函数
,且函数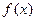 的值域为
的值域为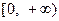 ,求
,求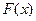 的表达式;
的表达式;
(2)在(1)的条件下,当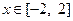 时,
时,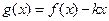 是单调函数,求实数
是单调函数,求实数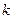 的取值范围;
的取值范围;
(3)设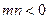 ,
,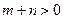 ,
,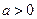 ,且函数
,且函数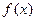 为偶函数,判断
为偶函数,判断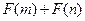 是否大于
是否大于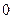 ?
?
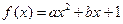 (
(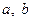 为实数,
为实数,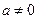 ,
,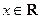 ),
),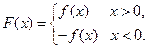
(1)若
 ,且函数
,且函数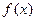 的值域为
的值域为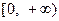 ,求
,求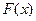 的表达式;
的表达式;(2)在(1)的条件下,当
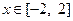 时,
时,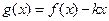 是单调函数,求实数
是单调函数,求实数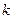 的取值范围;
的取值范围;(3)设
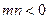 ,
,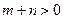 ,
,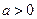 ,且函数
,且函数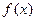 为偶函数,判断
为偶函数,判断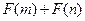 是否大于
是否大于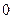 ?
?解:(Ⅰ)因为 ,所以
,所以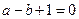 .
.
因为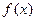 的值域为
的值域为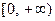 ,所以
,所以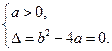 ……… 2分
……… 2分
所以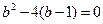 .解得
.解得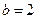 ,
,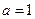 .所以
.所以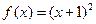 .
.
所以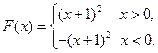 ………… 4分
………… 4分
(Ⅱ)因为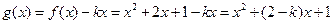
=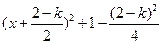 , ……… 6分
, ……… 6分
所以当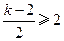 或
或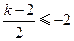 时
时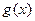 单调.
单调.
即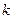 的范围是
的范围是 或
或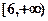 时,
时,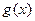 是单调函数. … 8分
是单调函数. … 8分
(Ⅲ)因为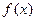 为偶函数,所以
为偶函数,所以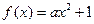 .
.
所以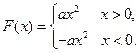 …………… 10分
…………… 10分
因为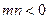 , 依条件设
, 依条件设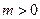 ,则
,则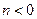 .
.
又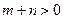 ,所以
,所以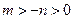 .
.
所以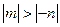 . ……………… 12分
. ……………… 12分
此时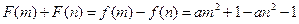
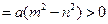 .
.
即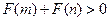 .
.
 ,所以
,所以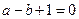 .
.因为
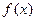 的值域为
的值域为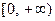 ,所以
,所以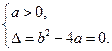 ……… 2分
……… 2分所以
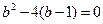 .解得
.解得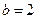 ,
,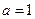 .所以
.所以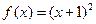 .
.所以
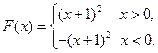 ………… 4分
………… 4分(Ⅱ)因为
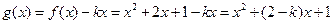
=
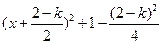 , ……… 6分
, ……… 6分所以当
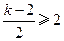 或
或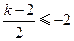 时
时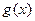 单调.
单调.即
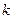 的范围是
的范围是 或
或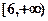 时,
时,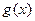 是单调函数. … 8分
是单调函数. … 8分(Ⅲ)因为
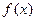 为偶函数,所以
为偶函数,所以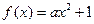 .
.所以
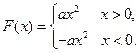 …………… 10分
…………… 10分因为
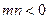 , 依条件设
, 依条件设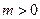 ,则
,则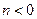 .
.又
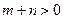 ,所以
,所以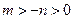 .
.所以
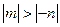 . ……………… 12分
. ……………… 12分此时
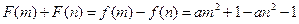
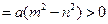 .
.即
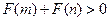 .
.
略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
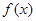 同时满足如下三个条件,求
同时满足如下三个条件,求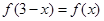 ;②
;②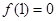 ;③对任意实数
;③对任意实数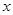 ,都有
,都有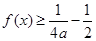 恒成立.
恒成立.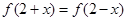 ,(2)被
,(2)被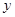 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式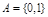 ,
,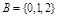 ,则从
,则从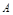 到
到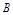 的映射有( )
的映射有( )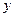 (万元)与年产量
(万元)与年产量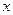 (吨)之间的函数关系式近似地表示为
(吨)之间的函数关系式近似地表示为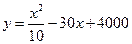 .问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
.问:(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润; 并求出最低成本。
并求出最低成本。
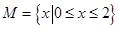 ,
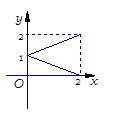
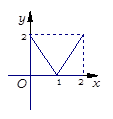
,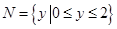 ,给出如下四个图形,其中能表
,给出如下四个图形,其中能表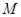 到集合
到集合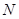 的函数关系的是 ( )
的函数关系的是 ( )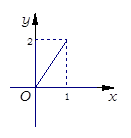
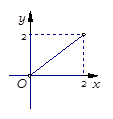
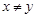 ,满足
,满足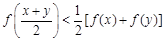 的函数
的函数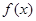 可以
可以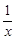
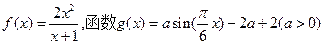 ,若存在
,若存在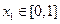 ,对任意
,对任意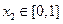 都有
都有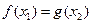 成立,则实数a的取值范围是 ( )
成立,则实数a的取值范围是 ( )