题目内容
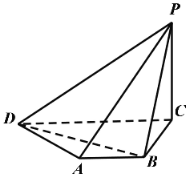
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是梯形,
是梯形,![]() //
//![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 是
是![]() 上的动点.
上的动点.
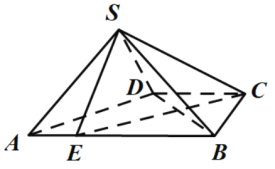
(1)试确定![]() 点的位置,使
点的位置,使![]() //平面
//平面![]() ;
;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)当![]() 时,
时,![]() 平面
平面![]() .(2)
.(2)![]()
【解析】
(1)当![]() 时,
时,![]() 平面
平面![]() .连接
.连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,由
,由![]() ,得
,得![]() ,得
,得![]() ,再由线面平行的判定可得
,再由线面平行的判定可得![]() 平面
平面![]() ;
;
(2)推导出![]() 平面
平面![]() ,以
,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,利用向量法能求出直线
,利用向量法能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
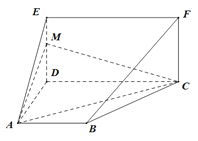
解:(1)当![]() 时,
时,![]() 平面
平面![]() .
.
证明如下:
连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
由于![]() ,
,![]()
所以![]()
![]()
![]() ,
,
又![]() ,所以
,所以![]()
所以![]() ,
,
由于![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;

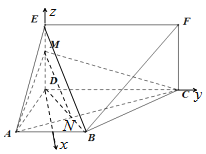
(2)因为平面![]() 平面
平面![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向,建立如图空间直角坐标系
轴的正方向,建立如图空间直角坐标系![]() .设
.设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由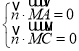 得,
得,![]()
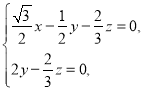 取
取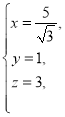 得
得![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则
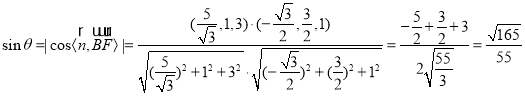 ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.