题目内容
以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线的位置关系是 ( )
| A.相离 | B.相切 | C.相交 | D.不能确定 |
B
不妨设抛物线为标准抛物线:y2="2px" (p>0 ),即抛物线位于Y轴的右侧,以X轴为对称轴.
设过焦点的弦为PQ,PQ的中点是M,M到准线的距离是d.
而P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.
又M到准线的距离d是梯形的中位线,故有d=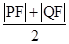 ,
,
由抛物线的定义可得: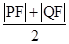 =
=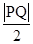 =半径.
=半径.
所以圆心M到准线的距离等于半径,
所以圆与准线是相切.
故答案为B.
设过焦点的弦为PQ,PQ的中点是M,M到准线的距离是d.
而P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.
又M到准线的距离d是梯形的中位线,故有d=
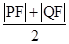 ,
,由抛物线的定义可得:
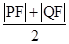 =
=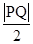 =半径.
=半径.所以圆心M到准线的距离等于半径,
所以圆与准线是相切.
故答案为B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
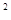 =4x的焦点坐标为
=4x的焦点坐标为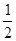 B.x=
B.x=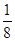 D.y=-
D.y=-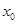 ,
,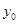 )为抛物线C:
)为抛物线C: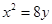 上一点,F为抛物线C的焦点,以F为圆心、
上一点,F为抛物线C的焦点,以F为圆心、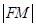 为半径的圆和抛物线C的准线相交,则
为半径的圆和抛物线C的准线相交,则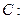
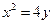 ,直线
,直线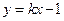 与
与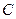 交于第一象限的两点
交于第一象限的两点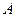 、
、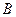 ,
,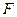 是
是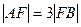 ,则
,则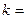
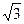 ?
?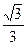
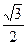

 分抛物线
分抛物线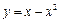 与x轴所围图形为面积相等的两部分,求k的值.
与x轴所围图形为面积相等的两部分,求k的值.
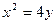 ,过点
,过点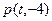 作抛物线的两条切线
作抛物线的两条切线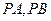 ,切点分别为
,切点分别为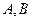 .
.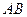 过定点
过定点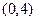 ;
;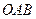 (
(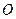 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.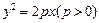 的焦点
的焦点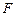 为双曲线
为双曲线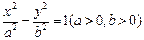 的一个焦点,经过两曲线交点的直线恰好过点
的一个焦点,经过两曲线交点的直线恰好过点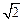

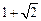
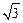
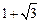
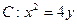 上一点P到定点A(0,1)的距离为2,则点P到
上一点P到定点A(0,1)的距离为2,则点P到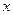 轴的距离为__________.
轴的距离为__________.