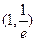题目内容
已知函数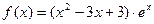 的定义域为[-2,t](t>-2),
的定义域为[-2,t](t>-2),
(Ⅰ)试确定t的取值范围,使得函数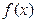 在[-2,t]上为单调函数;
在[-2,t]上为单调函数;
(Ⅱ)求证:对于任意的t>-2,总存在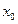 ∈(-2,t),满足
∈(-2,t),满足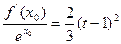 ,
,
并确定这样的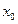 的个数.
的个数.
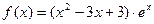 的定义域为[-2,t](t>-2),
的定义域为[-2,t](t>-2),(Ⅰ)试确定t的取值范围,使得函数
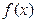 在[-2,t]上为单调函数;
在[-2,t]上为单调函数;(Ⅱ)求证:对于任意的t>-2,总存在
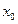 ∈(-2,t),满足
∈(-2,t),满足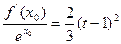 ,
,并确定这样的
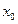 的个数.
的个数.(1)-2<t≤0(2)略
(1) 因为f′(x)=(x2-3x+3)·ex+(2x-3)·ex=x(x-1 )·ex,
)·ex,
由f′(x)>0⇒x>1或x<0;由f′(x)<0⇒0<x<1,
所以f(x)在(-∞,0),(1,+∞)上递增,在(0,1)上递减.
若f(x)在[-2,t]上为单调函数,则-2<t≤0
(2)证明:因为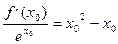 ,所以
,所以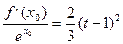 即为x-x0=(t-
即为x-x0=(t- 1)2,
1)2,
令g(x)=x2-x-(t-1)2,从而问题转化为证明方程
g(x)=x2-x-(t-1)2=0在(-2,t)上有解,并讨论解的个数.
因为g(-2)=6-(t-1)2=-(t+2)(t-4),
g(t)=t(t-1)-(t-1)2=(t+2)(t-1),
①当t>4或-2<t<1时,g(-2)·g(t)<0,
所以g(x)=0在(-2,t)上有解,且只有一解;
②当1<t<4时,g(-2)>0且g(t)>0,但由于g(0)=-(t-1)2<0,
所以g(x)=0在(-2,t)上有解,且有两解;
③当t=1时,g(x)=x2-x=0⇒x=0或x=1,
所以g(x)=0在(-2,t)上有且只有一解;
当t=4时,g(x )=x2-x-6=0⇒x=-2或x=3,
)=x2-x-6=0⇒x=-2或x=3,
所以g(x)=0在(-2,4)上也有且 只有一解.
只有一解.
综上所述,对于任意的t>-2,总存在x0∈(-2,t),满足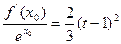 且当t≥4或-2<t≤1时,有唯一的x0适合题意;当1<t<4时,有两个x0适合题意.
且当t≥4或-2<t≤1时,有唯一的x0适合题意;当1<t<4时,有两个x0适合题意.
 )·ex,
)·ex,由f′(x)>0⇒x>1或x<0;由f′(x)<0⇒0<x<1,
所以f(x)在(-∞,0),(1,+∞)上递增,在(0,1)上递减.
若f(x)在[-2,t]上为单调函数,则-2<t≤0
(2)证明:因为
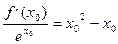 ,所以
,所以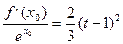 即为x-x0=(t-
即为x-x0=(t- 1)2,
1)2,令g(x)=x2-x-(t-1)2,从而问题转化为证明方程

g(x)=x2-x-(t-1)2=0在(-2,t)上有解,并讨论解的个数.
因为g(-2)=6-(t-1)2=-(t+2)(t-4),
g(t)=t(t-1)-(t-1)2=(t+2)(t-1),
①当t>4或-2<t<1时,g(-2)·g(t)<0,
所以g(x)=0在(-2,t)上有解,且只有一解;
②当1<t<4时,g(-2)>0且g(t)>0,但由于g(0)=-(t-1)2<0,
所以g(x)=0在(-2,t)上有解,且有两解;
③当t=1时,g(x)=x2-x=0⇒x=0或x=1,
所以g(x)=0在(-2,t)上有且只有一解;
当t=4时,g(x
 )=x2-x-6=0⇒x=-2或x=3,
)=x2-x-6=0⇒x=-2或x=3,所以g(x)=0在(-2,4)上也有且
 只有一解.
只有一解. 综上所述,对于任意的t>-2,总存在x0∈(-2,t),满足
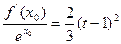 且当t≥4或-2<t≤1时,有唯一的x0适合题意;当1<t<4时,有两个x0适合题意.
且当t≥4或-2<t≤1时,有唯一的x0适合题意;当1<t<4时,有两个x0适合题意.
练习册系列答案
相关题目
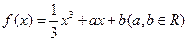 在
在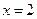 处取到极小值
处取到极小值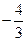 .
.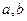 的值及函数
的值及函数 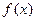 的单调区间;
的单调区间;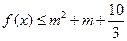 对
对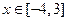 恒成立,求实数
恒成立,求实数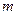 的取值范围.
的取值范围.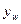 (万元)与投入资金
(万元)与投入资金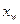 (万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润
(万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润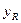 (万元)与投入资金
(万元)与投入资金 (万元)的关系满足
(万元)的关系满足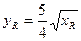 ,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)
,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元) 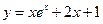 在点(0,1)处的切线方程为 .
在点(0,1)处的切线方程为 .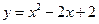 与
与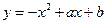
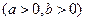 在它们的一个交点处切线互相垂直,则
在它们的一个交点处切线互相垂直,则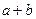 的值为
的值为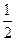
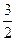
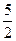
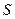 与时间
与时间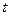 之间满足函数关系
之间满足函数关系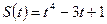 ,则该物体在
,则该物体在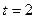 时的瞬时速度为( )
时的瞬时速度为( )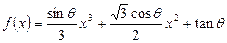 ,其中
,其中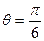 ,则导数
,则导数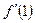 的值是( )
的值是( )



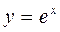 在点P处的切线斜率为e,则点P的坐标为( )
在点P处的切线斜率为e,则点P的坐标为( )