题目内容
在直角坐标平面中,△ABC的两个顶点为A(0,-1),B(0,1)平面内两点G、M同时满足①(1)求顶点C的轨迹E的方程.
(2)设P、Q、R、N都在曲线E上,定点F的坐标为(![]() ,0),已知
,0),已知![]() ∥
∥![]() ,
,![]() ∥
∥![]() 且
且![]() ·
·![]() =0.
=0.
求四边形PRQN面积S的最大值和最小值.
解:(1)设C(x,y),∵![]() +
+![]() =2
=2![]() ,由①知
,由①知![]() =-2
=-2![]() ,∴G为△ABC的重心,
,∴G为△ABC的重心,
∴G(![]() ,
,![]() ).
).
由②知M是△ABC的外心,∴M在x轴上由③知M(![]() ,0),由|
,0),由|![]() |=|
|=|![]() |得
|得![]() 化简整理得:
化简整理得:![]() +y2=1(x≠0).
+y2=1(x≠0).
(2)F(![]() ,0)恰为
,0)恰为![]() +y2=1的右焦点设PQ的斜率为k≠0且k≠±
+y2=1的右焦点设PQ的斜率为k≠0且k≠±![]() ,则直线PQ的方程为y=k(x-
,则直线PQ的方程为y=k(x-![]() ).
).
由
![]()
(3k2+1)x2-6![]() k2x+6k2-3=0.设P(x1,y1),Q(x2,y2)则x1+x2=
k2x+6k2-3=0.设P(x1,y1),Q(x2,y2)则x1+x2=![]() ,x1·x2=
,x1·x2=![]() .
.
则|PQ|=![]() ·
·![]() =
=![]() ·
·![]() =
=![]() .
.
∵PN⊥PQ,把k换成-![]() 得|RN|=
得|RN|=![]() .
.
∴S=![]() |PQ|·|RN|=
|PQ|·|RN|=![]() =2-
=2-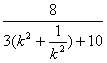 .∴3(k2+
.∴3(k2+![]() )+10=
)+10=![]() .∵k2+
.∵k2+![]() ≥2,∴
≥2,∴![]() ≥16,∴
≥16,∴![]() ≤S<2,(当k=±1时取等号)又当k不存在或k=0时,S=2.综上可得
≤S<2,(当k=±1时取等号)又当k不存在或k=0时,S=2.综上可得![]() ≤S≤2.
≤S≤2.
∴Smax=2,Smin=![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目