题目内容
(本小题满分14分)
某工厂生产A、B型两类产品，每个产品需粗加工和精加工两道工序完成. 已知粗加工做一个A、B型产品分别需要1小时和2小时，精加工一个A、B型产品分别需要3小时和1小时；又知粗加工、精加工每天工作分别不得超过8小时和9小时，而工厂生产一个A、B型产品分别获利润200元和300元，试问工厂每天应生产A、B型产品各多少个，才能获得利润最大？
解：设每天生产A型产品x个，B型产品子y个， ------- 1分
则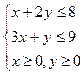
-------------5分
目标函数为：z=2x+3y ---------------6分
作出可行域：
把直线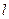
：2x+3y=0向右上方平移至
的位置时，直线经过可行域上的点M，且与原点距
离最大，此时z=2x+3y取最大值
----------------------11分
解方程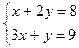
得M的坐标为（2，3）. -------13分
答：每天应生产A型产品2个，B型产品3个才能获得最大利润 -----14分
（画图正确给 10分）
解析
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）