题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≤0)}\\{f(x-1)+1(x>0)}\end{array}\right.$,g(x)=f(x)-x,把函数g(x)的零点按从小到大的顺序排列成一个数列,则该数的前n项和为( )| A. | Sn=$\frac{n(n-1)}{2}$ | B. | Sn=$\frac{n(n+1)}{2}$ | C. | Sn=2n-1 | D. | Sn=2n-1-1 |
分析 根据解析式函数f(x)得出归纳推理得出f(n)=n,n∈N,得出g(x)的零点为:0,1,2,3,4…n-1,运用等差数列的知识求解即可.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≤0)}\\{f(x-1)+1(x>0)}\end{array}\right.$,
∴f(0)=0,f(1)=f(0)+1=1,f(2)=f(1)+1=2,
f(3)=f(2)+1=3,
归纳推理得出f(n)=n,n∈N
∵g(x)=f(x)-x,
∴g(x)的零点为:0,1,2,3,4…n-1,
∵函数g(x)的零点按从小到大的顺序排列成一个数列,
∴该数的前n项和为:$\frac{n(0+n-1)}{2}$=$\frac{n(n-1)}{2}$
故选:A
点评 本题考查了函数的性质,零点的问题,融合了数列的知识,综合性较强,难度较大,属于中档题.

练习册系列答案
相关题目
9.设i为虚数单位,复数z=(1+i)2+2,则z的共轭复数为( )
| A. | -2i | B. | 2i | C. | 2-2i | D. | 2+2i |
7.设复数z1=1-i,z2=$\sqrt{3}$+i,其中i为虚数单位,则$\frac{\overline{{z}_{1}}}{{z}_{2}}$的虚部为( )
| A. | $\frac{1+\sqrt{3}}{4}i$ | B. | $\frac{1+\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}-1}{4}i$ | D. | $\frac{\sqrt{3}-1}{4}$ |
14.已知m,n是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是( )
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
11.已知不等式x2-ax+a-2>0(a>2)的解集为(-∞,x1)∪(x2,+∞),则x1+x2+$\frac{1}{{x}_{1}{x}_{2}}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
3.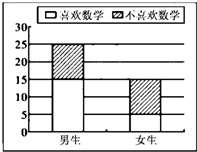 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
(Ⅰ)根据图中相关数据完成以下2×2列联表;并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”?
(Ⅱ)从该班所有女生中随机选取2人交流学习体会,求这2人中喜欢数学课程的人数X的分布列和数学期望.
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.(Ⅰ)根据图中相关数据完成以下2×2列联表;并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”?
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |