题目内容
10.已知Ω是不等式组$\left\{\begin{array}{l}{x+y<6}\\{x>0}\\{y>0}\end{array}\right.$表示的平面区域,A是不等式组$\left\{\begin{array}{l}{x<4}\\{y>0}\\{x-2y>0}\end{array}\right.$表示的平面区域,若向区域Ω上随机投一点P,则点P落入区域A的概率为$\frac{2}{9}$.分析 分别画出两个区域对应的图形,求出面积,利用几何概型公式解答.根据二元一次不等式组表示的平面区域的原理,分别作出集合Ω和集合A对应的平面区域,得到它们都直角三角形.计算出这两个直角三角形的面积后,再用符合题的面积即小三角形面积,除以整个图形即大三角形的面积得到概率
解答  解:区域Ω是不等式组$\left\{\begin{array}{l}{x+y<6}\\{x>0}\\{y>0}\end{array}\right.$表示的平面区域如图三角形区域OEF,面积为$\frac{1}{2}×6×6=18$;
解:区域Ω是不等式组$\left\{\begin{array}{l}{x+y<6}\\{x>0}\\{y>0}\end{array}\right.$表示的平面区域如图三角形区域OEF,面积为$\frac{1}{2}×6×6=18$;
A是不等式组$\left\{\begin{array}{l}{x<4}\\{y>0}\\{x-2y>0}\end{array}\right.$表示的平面区域,如图阴影部分,面积为$\frac{1}{2}×4×2$=4,
由几何概型公式可得点P落入区域A的概率为:$\frac{4}{18}=\frac{2}{9}$;
故答案为:$\frac{2}{9}$.
点评 本题着重考查了二元一次不等式组表示的平面区域和几何概率模型.准确画作相应的平面区域,熟练地运用面积比求相应的概率,是解决本题的关键

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
20.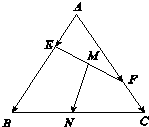 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
18.若向量$\overrightarrow{a}$=(2,x+1),$\overrightarrow{b}$=(x+2,6),又$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角,则实数x的取值范围为( )
| A. | {x|x>-$\frac{5}{4}$且x≠2} | B. | {x|x>-$\frac{5}{4}$} | C. | {x|x<-$\frac{5}{4}$且x≠-5} | D. | {x|x<-$\frac{5}{4}$} |
2.阅读如图的程序框图,当程序运行后,输出S的值为( )
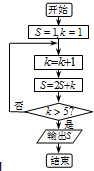

| A. | 57 | B. | 119 | C. | 120 | D. | 247 |
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≤0)}\\{f(x-1)+1(x>0)}\end{array}\right.$,g(x)=f(x)-x,把函数g(x)的零点按从小到大的顺序排列成一个数列,则该数的前n项和为( )
| A. | Sn=$\frac{n(n-1)}{2}$ | B. | Sn=$\frac{n(n+1)}{2}$ | C. | Sn=2n-1 | D. | Sn=2n-1-1 |
 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.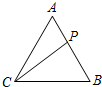 如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.
如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.