题目内容
若实数a,b,c,d满足︱b+a2-3lna︱+(c-d+2)2=0,则(a-c)2+(b-d)2的最小值为 .
8
解析∵实数a、b、c、d满足:(b+a2-3lna)2+(c-d+2)2=0,∴b+a2-3lna=0,c-d+2=0,设b=y,a=x,则y=3lnx-x2,设c=x,d=y,则y=x+2,
∴(a-c)2+(b-d)2就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值.对曲线y=3lnx-x2求导:y'(x)=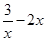 ,与y=x+2平行的切线斜率k=1=
,与y=x+2平行的切线斜率k=1=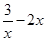 ,解得x=1或x=-
,解得x=1或x=- (舍)
(舍)
把x=1代入y=3lnx-x2,得y=-1,即切点为(1,-1)切点到直线y=x+2的距离:
∴(a-c)2+(b-d)2的最小值就是8.
考点:导数在最大值、最小值问题中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
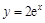 相切,则实数k = .
相切,则实数k = .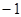 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .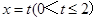 左侧的图形的面积为
左侧的图形的面积为 ,则
,则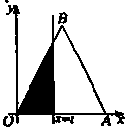
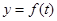 的图像与直线
的图像与直线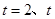 轴围成的图形面积为______.
轴围成的图形面积为______.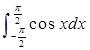 的值为2;②若
的值为2;②若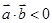 ,则
,则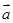 与
与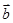 的夹角为钝角;③若
的夹角为钝角;③若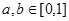 ,则不等式
,则不等式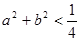 成立的概率是
成立的概率是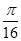 ;④函数
;④函数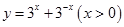 的最小值为2.
的最小值为2.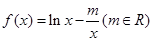 在区间
在区间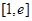 上取得最小值4,则
上取得最小值4,则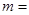 ___________.
___________.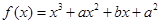 .在
.在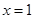 处有极值10,则
处有极值10,则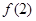 等于_______.
等于_______.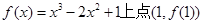 处的切线方程为 。
处的切线方程为 。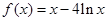 ,则曲线
,则曲线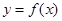 在点
在点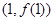 处的切线方程为___________.
处的切线方程为___________.