题目内容
已知函数f(x)=eax-x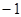 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .

解析试题分析:试题分析:若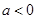 ,则对一切
,则对一切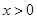 ,
,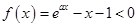 ,这与题设矛盾.又
,这与题设矛盾.又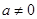 ,故
,故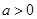 .
.
而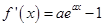 ,令
,令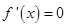 得
得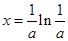 .
.
当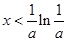 时,
时,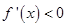 ,
,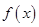 单调递减;当
单调递减;当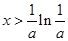 时,
时,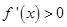 ,
,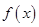 单调递增.故当x
单调递增.故当x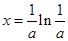 ,
,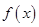 取最小值
取最小值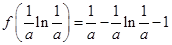 .
.
于是对一切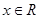 ,
,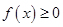 恒成立,当且仅当
恒成立,当且仅当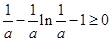 . ①
. ①
令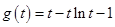 ,则
,则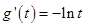 .
.
当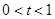 时,
时,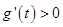 ,
,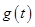 单调递增;当
单调递增;当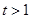 时,
时,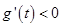 ,
,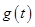 单调递减.
单调递减.
故当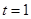 时,
时,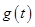 取最大值
取最大值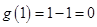 .
.
因此,当且仅当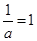 ,即
,即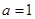 时,①式成立.综上所述,
时,①式成立.综上所述, 的取值集合为
的取值集合为 .
.
考点:用导数研究函数的单调性及最值问题。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 与
与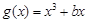 的图象在
的图象在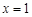 处有相同的切线,
处有相同的切线, = .
= .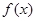 的定义域为R,
的定义域为R, 为
为 的图象如图所示,且
的图象如图所示,且 ,
, ,则不等式
,则不等式 的解集为
的解集为 
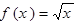 在
在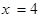 处的切线方程___________
处的切线方程___________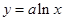
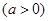 在
在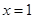 处的切线与两坐标轴围成的三角形的面积为4,则
处的切线与两坐标轴围成的三角形的面积为4,则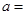 .
. x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则a的取值范围为________.
,+∞)上存在单调递增区间,则a的取值范围为________.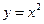 ,如图所示,若使图中的阴影部分的面积
,如图所示,若使图中的阴影部分的面积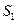 与
与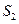 之和最小,则此区间内的t= 。
之和最小,则此区间内的t= 。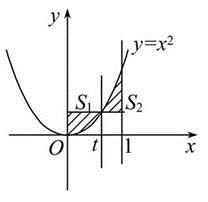
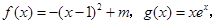 若
若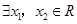 ,使得
,使得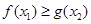 成立,则实数
成立,则实数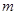 的取值范围是_______.
的取值范围是_______.