题目内容
已知函数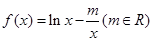 在区间
在区间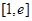 上取得最小值4,则
上取得最小值4,则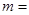 ___________.
___________.
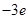
解析试题分析:函数 的定义域为
的定义域为 ,
,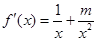 .当
.当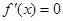 时,
时, ,此时
,此时 .当
.当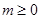 ,无解.所以,当
,无解.所以,当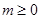 时,
时,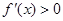 ,
, 为增函数,所以
为增函数,所以 ,
, ,矛盾舍去;当
,矛盾舍去;当 时,若
时,若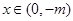 ,
, ,
, 为减函数,若
为减函数,若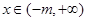 ,
,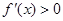 ,
, 为增函数,所以
为增函数,所以 为极小值,也是最小值;①当
为极小值,也是最小值;①当 ,即
,即 时,
时, 在
在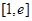 上单调递增,所以
上单调递增,所以 ,所以
,所以 (矛盾);②当
(矛盾);②当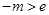 ,即
,即 时,
时, 在
在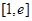 上单调递减,
上单调递减, ,所以
,所以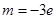 .③当
.③当 ,即
,即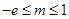 时,
时, 在
在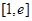 上的最小值为
上的最小值为 ,此时
,此时 (矛盾).综上
(矛盾).综上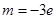 .
.
考点:1、导数与函数的单调性、极值、最值的关系;2、不等式解法;3、对数运算.

练习册系列答案
相关题目
 ,当
,当 时,给出下列几个结论:
时,给出下列几个结论: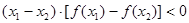 ;②
;②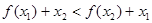 ;③
;③ ;
; 时,
时, .
.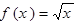 在
在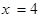 处的切线方程___________
处的切线方程___________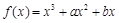 为奇函数,其图象的一条切线方程为
为奇函数,其图象的一条切线方程为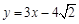 ,则b的值为 .
,则b的值为 . ,设曲线
,设曲线 在点
在点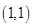 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为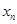 ,令
,令
 ,则
,则 .
. =_________.
=_________.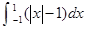 的值为____________.
的值为____________.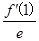 ex-f(0)x+
ex-f(0)x+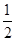 x2在点(1,f(1))处的切线方程为________.
x2在点(1,f(1))处的切线方程为________.