题目内容
(文科只做(1)(2)问,理科全做)
设 是函数
是函数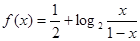 图象上任意两点,且
图象上任意两点,且 ,已知点
,已知点 的横坐标为
的横坐标为 ,且有
,且有 ,其中
,其中 且n≥2,
且n≥2,
(1) 求点 的纵坐标值;
的纵坐标值;
(2) 求 ,
, ,
,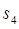 及
及 ;
;
(3)已知 ,其中
,其中 ,且
,且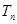 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 都成立,试求λ的最小正整数值。
都成立,试求λ的最小正整数值。
(1)M点的纵坐标为定值 ;
;
(2)
(3) 的最小正整数为1。
的最小正整数为1。
解析试题分析:(1)依题意由 知M为线段AB的中点。
知M为线段AB的中点。
又 的横坐标为1,A
的横坐标为1,A ,B
,B 即
即

即M点的纵坐标为定值 (理3分) (文4分)
(理3分) (文4分)
(2) (文6分)
(文6分) (文8分)
(文8分) ……(文8分)(理2小题共5分)
……(文8分)(理2小题共5分)
由①知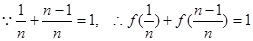

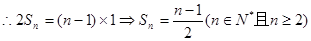 (文14分)
(文14分)
(3)当 时,
时,
又 ,
, 也适合。
也适合。 


由 恒成立
恒成立
而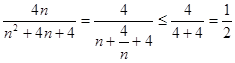 (当且仅当
(当且仅当 取等号)
取等号) ,
, 的最小正整数为1(理14分)
的最小正整数为1(理14分)
考点:本题主要考查函数的概念,对数函数的图象和性质,数列的概念,不等式恒成立问题。
点评:难题,本题综合考查函数的概念,对数函数的图象和性质,数列的概念,不等式恒成立问题。难度较大,对于不等式恒成立问题,往往通过构造函数,确定函数的最值,使问题得解。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的前
的前 项和
项和 (
( ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,试比较
,试比较 与
与 的大小,并予以证明
的大小,并予以证明 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前
的前 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 满足
满足

 ,求数列
,求数列 的前n项和
的前n项和
 ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。 }满足a
}满足a =2a
=2a +a
+a ,且a
,且a +a
+a =2a
=2a +4,其中n∈N
+4,其中n∈N .
. ,求数列{b
,求数列{b +
+ +…+
+…+ >
> (n≥2).
(n≥2). x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
 ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。 ,{bn}的前n项和为Sn,求证
,{bn}的前n项和为Sn,求证