题目内容
(2011•潍坊二模)已知函数f(x)=a(x-
)-2lnx,g(x)=x2.
(I)若函数f(x)在其定义域上为增函数,求实数a的取值范围;
(Ⅱ)若函数f(x)与g(x)的图象在其一公共点处存在公切线,证明:a=2e
-1.
| 1 |
| x |
(I)若函数f(x)在其定义域上为增函数,求实数a的取值范围;
(Ⅱ)若函数f(x)与g(x)的图象在其一公共点处存在公切线,证明:a=2e
| a2 |
| 8 |
分析:(I)求函数的导数,若函数f(x)在其定义域上为增函数,则f'(x)≥0恒成立,然后求实数a的取值范围;
(Ⅱ)利用导数的几何意义求函数f(x)与g(x)的共切线,然后证明等式.
(Ⅱ)利用导数的几何意义求函数f(x)与g(x)的共切线,然后证明等式.
解答:解:(I)函数f(x)的定义域为(0,+∞),函数的导数为f′(x)=a+
-
=
.
要使函数f(x)在其定义域上为增函数,f'(x)≥0恒成立,即ax2-2x+a≥0,在(0,+∞)上恒成立.
即a≥
在(0,+∞)上恒成立.
因为
=
≤
=1,当且仅当x=1时取等号,所以a≥1.
(Ⅱ)因为函数的导数为f′(x)=a+
-
=
,
g'(x)=2x,令
=2x,
即2x3-ax2+2x-a=0,所以x2(2x-a)+2x-a=0,即(x2+1)(2x-a)=0,
所以2x-a=0,x=
.
因为f(x)=a(x-
)-2lnx,
则f(
)=a(
-
)-2ln
=
a2-2ln
-2,
对于g(x)=x2.则g(
)=
.
因为g(
)=f(
),所以
a2-2ln
-2=
,即a2-8ln
-8=0.
所以a2-8=8ln
,
=ln
,
即
-1=ln
,
解得
=e
-1,
所以a=2e
-1,成立.
| a |
| x2 |
| 2 |
| x |
| ax2-2x+a |
| x2 |
要使函数f(x)在其定义域上为增函数,f'(x)≥0恒成立,即ax2-2x+a≥0,在(0,+∞)上恒成立.
即a≥
| 2x |
| x2+1 |
因为
| 2x |
| x2+1 |
| 2 | ||
x+
|
| 2 |
| 2 |
(Ⅱ)因为函数的导数为f′(x)=a+
| a |
| x2 |
| 2 |
| x |
| ax2-2x+a |
| x2 |
g'(x)=2x,令
| ax2-2x+a |
| x2 |
即2x3-ax2+2x-a=0,所以x2(2x-a)+2x-a=0,即(x2+1)(2x-a)=0,
所以2x-a=0,x=
| a |
| 2 |
因为f(x)=a(x-
| 1 |
| x |
则f(
| a |
| 2 |
| a |
| 2 |
| 2 |
| a |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
对于g(x)=x2.则g(
| a |
| 2 |
| a2 |
| 4 |
因为g(
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
所以a2-8=8ln
| a |
| 2 |
| a2-8 |
| 8 |
| a |
| 2 |
即
| a2 |
| 8 |
| a |
| 2 |
解得
| a |
| 2 |
| a2 |
| 8 |
所以a=2e
| a2 |
| 8 |
点评:本题主要考查了利用导数研究函数的单调性,综合性较强运算量较大,考查学生的运算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
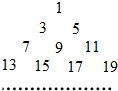 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足