题目内容
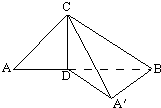 CD是直角三角形ABC斜边上的高,BD=2AD,将△ACD绕CD旋转到△A′CD,使二面角A′-CD-B为60°.
CD是直角三角形ABC斜边上的高,BD=2AD,将△ACD绕CD旋转到△A′CD,使二面角A′-CD-B为60°.(1)求证:BA′⊥面A′CD;
(2)求异面直线A′C与BD所成角的余弦.
分析:(1)要证明线面垂直常采用线面垂直的判定定理证明即可根据CD是直角三角形ABC斜边上的高得出CD⊥A′B再根据将△ACD绕CD旋转到△A′CD,使二面角A′-CD-B为60°且BD=2AD可得出△BAA′D为直角三角形即A′D⊥A′B然后根据线面垂直的判定定理即可得证.
(2)根据异面直线所成的角的定义可过A'作BD的平行线A′E然后构造平行四边形A′BDE则根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角然后再利用余弦定理求解即可.
(2)根据异面直线所成的角的定义可过A'作BD的平行线A′E然后构造平行四边形A′BDE则根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角然后再利用余弦定理求解即可.
解答:证明:(1)∵BD=2AD
∴BD=2AD
∵二面角A′-CD-B为60°,∠BDA为二面角A′-CD-B的平面角
∴∠BDA=60°
∴△BAA′D为直角三角形
∴A′D⊥A′B
又∵CD⊥A′B,CD∩A′D=D
∴BA′⊥面A′CD
(2)过A′作BD的平行线A′E然后构造平行四边形BA′DE
∴根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角
设AD=1
∴BD=2,A′B=
,CD=
,A′D=1,CE=
∴由余弦定理得:cos∠CA′E=
=
即异面直线A′C与BD所成角的余弦为
∴BD=2AD
∵二面角A′-CD-B为60°,∠BDA为二面角A′-CD-B的平面角
∴∠BDA=60°
∴△BAA′D为直角三角形
∴A′D⊥A′B
又∵CD⊥A′B,CD∩A′D=D
∴BA′⊥面A′CD
(2)过A′作BD的平行线A′E然后构造平行四边形BA′DE
∴根据异面直线所成的角的定义可得∠CA′E异面直线A′C与BD所成角
设AD=1
∴BD=2,A′B=
| 3 |
| 2 |
| 5 |
∴由余弦定理得:cos∠CA′E=
| A′C2+A′E2- EC2 |
| 2A′C•A′E |
| ||
| 6 |
即异面直线A′C与BD所成角的余弦为
| ||
| 6 |
点评:本题主要考察了线面垂直的证明和异面直线所成的角的求解,属常考题型,较难.解题的关键是要掌握线面垂直证明的常用方法:线面垂直的判定定理或向量法而异面直线所成的角的求解常用定义法或向量法!

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
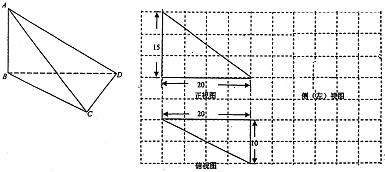 如图,在三棱锥A-BCD中,AB⊥平面BCD,它的正视图和俯视图都是直角三角形,图中尺寸单位为cm.
如图,在三棱锥A-BCD中,AB⊥平面BCD,它的正视图和俯视图都是直角三角形,图中尺寸单位为cm.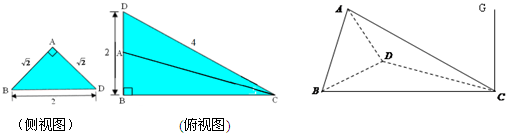
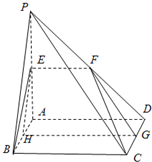 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G,H分别是线段PA,PD,CD,AB的中点.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G,H分别是线段PA,PD,CD,AB的中点.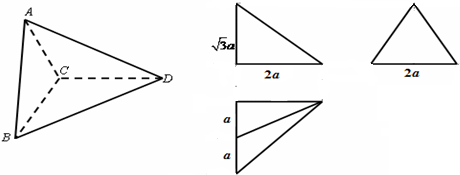 某几何体的直观图与三视图如下,其中主视图、俯视图都是直角三角形,左视图是等边三角形.
某几何体的直观图与三视图如下,其中主视图、俯视图都是直角三角形,左视图是等边三角形.