题目内容
11.已知函数f(x)=xlnx.(题中e=2.71828为自然对数的底数)(1)若方程f(x)-a=0在区间$[\frac{1}{e^2},+∞)$上有2个不同的实根,求实数a的取值范围;
(2)点P(x0,y0)(x0>$\frac{1}{e}$)是函数f(x)的图象上一动点,求函数f(x)的图象上点P处的切线与两坐标轴围成三角形面积的最小值;
(3)设g(x)=f(x)-$\frac{1}{e}{x^2}$,证明:g(x)极小值>$\frac{1-e}{e}$.
分析 (1)求出函数的导数,利用导数和极值之间的关系求出函数的极值即可.
(2)求出函数的导数,利用导数的几何意义求出函数的切线方程即可.
(3)求出函数的导数,利用导数求出函数的极值,利用不等式的性质进行证明.
解答 解:(1)令f'(x)=1+lnx<0,得$x<\frac{1}{e}$,
令f'(x)=1+lnx>0,得$x>\frac{1}{e}$,
∴f(x)在$[\frac{1}{e^2},\frac{1}{e})$上单调递减,在$(\frac{1}{e},+∞)$上单调递增,…(2分)
又$f(\frac{1}{e^2})=-\frac{2}{e^2}$,$f(\frac{1}{e})=-\frac{1}{e}$,要方程f(x)-a=0在区间$[\frac{1}{e^2},+∞)$上有2个不同的实根,则$f(\frac{1}{e})<a≤f(\frac{1}{e^2})$,即$a∈(-\frac{1}{e},-\frac{1}{e^2}]$…(4分)
(2)点P(x0,y0)处的切线为y-y0=(1+lnx0)(x-x0),
令x=0,得y=-x0,令y=0,得$x=\frac{x_0}{{1+ln{x_0}}}$,
∴$S=\frac{1}{2}{x_0}•\frac{x_0}{{1+ln{x_0}}}=\frac{1}{2}•\frac{x_0^2}{{1+ln{x_0}}}$(${x_0}>\frac{1}{e}$)…(6分)
令$φ(x)=\frac{1}{2}•\frac{x^2}{1+lnx}$,
则$φ'(x)=\frac{x(2lnx+1)}{{2{{(1+lnx)}^2}}}>0⇒x>\frac{1}{{\sqrt{e}}}$,$φ'(x)=\frac{x(2lnx+1)}{{2{{(1+lnx)}^2}}}<0⇒\frac{1}{e}<x<\frac{1}{{\sqrt{e}}}$,
∴$φ{(x)_{min}}=φ(\frac{1}{{\sqrt{e}}})=\frac{1}{e}$∴${S_{min}}=\frac{1}{e}$.…(8分)
(3)$g(x)=xlnx-\frac{1}{e}{x^2}$,令$g'(x)=1+lnx-\frac{2}{e}x=0$,即$lnx=\frac{2}{e}x-1$(*)
易知方程(*)的一根为x=e,结合函数y=lnx与$y=\frac{2}{e}x-1$图象,
设另一根为x=x1,则$ln{x_1}=\frac{2}{e}{x_1}-1$,…(9分)
∵当x=1时,$ln1>\frac{2}{e}•1-1$,
∴0<x1<1,…(10分)
且当x∈(0,x1)时,g'(x)<0,
当x∈(x1,e)时,g'(x)>0,当x∈(e,+∞)时,g'(x)<0,
∴$g{(x)_{极小值}}=g({x_1})={x_1}ln{x_1}-\frac{1}{e}{x_1}^2={x_1}(\frac{2}{e}{x_1}-1)-\frac{1}{e}{x_1}^2=\frac{1}{e}x_1^2-{x_1}$…(12分)
∵x1∈(0,1),∴$g{(x)_{极小值}}>\frac{1}{e}×{1^2}-1=\frac{1-e}{e}$…(13分)
点评 本题主要考查导数的综合应用,要求熟练掌握函数的极值,最值和函数导数之间的关系,综合性较强,难度较大.

 名校课堂系列答案
名校课堂系列答案| A. | 已知a,b∈R,则“$\frac{{{a^2}+{b^2}}}{ab}≤-2$”是“a>0且b<0”的充分不必要条件 | |
| B. | 已知数列{an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | 已知两个平面α,β,若两条异面直线m,n满足m?α,n?β且m∥β,n∥α,则α∥β | |
| D. | ?x0∈(-∞,0),使${3^{x_0}}<{4^{x_0}}$成立 |
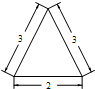
| A. | π | B. | 2π | C. | 3π | D. | 4π |
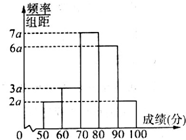 100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50.
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50.