题目内容

1．已知复数|$\overline{z}$-3+4i|=5，则z对应的点的轨迹方程为x2+y2-6x-8y=0．

分析 设出复数z，利用复数的模求解即可．

解答 解：设z=x+yi，
复数|$\overline{z}$-3+4i|=5，
可得（x-3）2+（-y+4）2=25，
即x2+y2-6x-8y=0．
故答案为：x2+y2-6x-8y=0．

点评 本题考查复数的几何意义，复数代数形式的混合运算，轨迹方程的求法，考查计算能力．

练习册系列答案
相关题目
11．计算：（1）lg2+lg5=1；
（2）log36-log32=1；
（3）log525=2；
（4）3log82=1；
（5）$\frac{1}{2}$lg4+lg5=1；
（6）log575-2log5$\sqrt{3}$=2；
（7）log5$\sqrt{3}$•2log3$\sqrt{5}$=$\frac{1}{2}$．
12．若直线f（x）=$\frac{1}{2}$x+t经过点P（1，0），且f（a）+f（2b）+f（3c）=-$\frac{1}{2}$，则当3a+2b+c=2时，a2+2b2+3c2取得最小值．
9．若曲线C1：y=$\frac{a}{2}$x2（a＞0）与曲线C2：y=ex存在公共切线，则实数a的取值范围是[$\frac{{e}^{2}}{2}$，+∞）．
16．已知函数f（x）=$\sqrt{3}$sin（2ωx-$\frac{π}{3}$）+$\frac{3}{2}$+t图象中，对称中心到对称轴的最小距离为$\frac{π}{4}$，且当x∈[0，$\frac{π}{3}$]时，f（x）的最大值为1．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调递增区间和对称轴．
6．已知复数z1、z2满足z1•$\overline{{z}_{2}}$≠0，|z1+z2|=|z1-z2|，求证：$\frac{{{z}_{1}}^{2}}{{{z}_{2}}^{2}}$＜0．
13．已知在各项均为正数的等比数列{an}中，a1a2=2，a3a4=32．
（1）求数列{an}的通项公式；
（2）设bn=（2n-1）an（n∈N*），求数列{bn}的前n项和Tn．
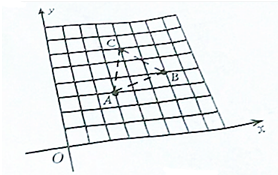10．如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为（3，3）、（6，4）、（4，6）．
（1）请直接写出这个平行四边形的第四个顶点的坐标；
（2）求这个平行四边形的面积．
11．已知函数f（x）=xlnx．（题中e=2.71828为自然对数的底数）
（1）若方程f（x）-a=0在区间$[\frac{1}{e^2}，+∞）$上有2个不同的实根，求实数a的取值范围；
（2）点P（x0，y0）（x0＞$\frac{1}{e}$）是函数f（x）的图象上一动点，求函数f（x）的图象上点P处的切线与两坐标轴围成三角形面积的最小值；
（3）设g（x）=f（x）-$\frac{1}{e}{x^2}$，证明：g（x）极小值＞$\frac{1-e}{e}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网