题目内容
有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问: 工人师傅是怎样选择矩形的四点的?并求出最大面积值.
矩形MNPQ为面积最大的矩形,面积最大值为 R2.
R2.
 R2.
R2. 如下图,扇形AOB的内接矩形是MNPQ,连OP,则OP=R,设∠AOP=θ,则∠
QOP=45°-θ,NP=Rsinθ,在△PQO中, ,
,
∴PQ= Rsin(45°-θ).
Rsin(45°-θ).
S矩形MNPQ=QP·NP= R2sinθsin(45°-θ)
R2sinθsin(45°-θ)
= R2·[cos(2θ-45°)-
R2·[cos(2θ-45°)- ]≤
]≤ R2,
R2,
当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为 R2.
R2.
工人师傅是这样选点的,记扇形为AOB,以扇形一半径OA为一边,在扇形上作角AOP且使∠AOP=22.5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为 R2.
R2.

QOP=45°-θ,NP=Rsinθ,在△PQO中,
 ,
,∴PQ=
 Rsin(45°-θ).
Rsin(45°-θ).S矩形MNPQ=QP·NP=
 R2sinθsin(45°-θ)
R2sinθsin(45°-θ)=
 R2·[cos(2θ-45°)-
R2·[cos(2θ-45°)- ]≤
]≤ R2,
R2,当且仅当cos(2θ-45°)=1,即θ=22.5°时,S矩形MNPQ的值最大且最大值为
 R2.
R2.工人师傅是这样选点的,记扇形为AOB,以扇形一半径OA为一边,在扇形上作角AOP且使∠AOP=22.5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为
 R2.
R2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16
16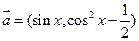 ,
,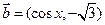 ,其中
,其中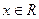 ,函数
,函数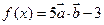
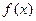 的最小正周期;
的最小正周期;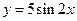 的图象经过怎样的变化而得到?
的图象经过怎样的变化而得到? )-
)- sin2x+sinxcosx
sin2x+sinxcosx ,
, ]时,f(x)的反函数为f-1(x),求f--1(1)的值。
]时,f(x)的反函数为f-1(x),求f--1(1)的值。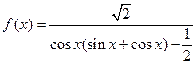 (I)求函数
(I)求函数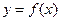 的周期;(II)设函数
的周期;(II)设函数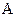 ,若
,若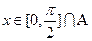 ,求函数
,求函数 已知向量
已知向量 ,
, .(1)若
.(1)若 ,试判断
,试判断 与
与 能否平行?(2)若
能否平行?(2)若 ,求函数
,求函数 的最小值.
的最小值. (米)是时间
(米)是时间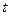 (0≤
(0≤
 的图像.
的图像.
 .
. 的值; (Ⅱ)设
的值; (Ⅱ)设 ,
, ,求
,求 的值.
的值. ,且
,且 ,则 ( )
,则 ( )



