题目内容
将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同盒子中的3个中,使得有1个空盒且其他3个盒子中球的颜色齐全的不同放法共有 种.(用数字作答)
720
解析试题分析:本题可以分步来做:
第一步:首先从4个盒子中选取3个,共有4种取法;
第二步:假定选取了前三个盒子,则第四个为空,不予考虑。由于前三个盒子中的球必须同时包含黑白红三色,所以我们知道,每个盒子中至少有一个白球,一个黑球和一个红球。
第三步:①这样,白球还剩一个可以自由支配,它可以放在三个盒子中任意一个,共3种放法。②黑球还剩两个可以自由支配,这两个球可以分别放入三个盒子中的任意一个,这里有两种情况:一是两个球放入同一个盒子,有3种放法;二是两个球放入不同的两个盒子,有3种放法。综上,黑球共6种放法。③红球还剩三个可以自由支配,分三种情况:一是三个球放入同一个盒子,有3中放法。二是两个球放入同一个盒子,另外一个球放入另一个盒子,有6种放法。三是每个 盒子一个球,只有1种放法。综上,红球共10种放法。
所以总共有4×3×6×10=720种不同的放法。
考点:排列、组合;分布乘法原理;分类加法原理。
点评:本题考查排列、组合的运用,注意本题中同色的球是相同的。对于较难问题,我们可以采取分步来做。

练习册系列答案
相关题目
 ,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为
,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为 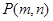 落在圆x2+y2=16内的概率是___________。
落在圆x2+y2=16内的概率是___________。 ,在区间
,在区间 上随机取一个数
上随机取一个数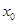 ,则使得
,则使得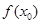 ≥0的概率为 .
≥0的概率为 .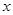 的一元二次方程
的一元二次方程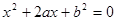
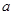 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,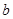 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;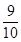 ,从中任意摸出2个球,得到的都是白球的概率为
,从中任意摸出2个球,得到的都是白球的概率为