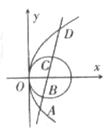
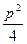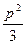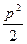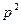题目内容
(本题满分13分)已知抛物线C的方程为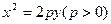 ,A,B是抛物线C上的两点,直线AB过点M
,A,B是抛物线C上的两点,直线AB过点M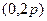 。(Ⅰ)设
。(Ⅰ)设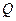 是抛物线上任意一点,求
是抛物线上任意一点,求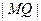 的最小值; (Ⅱ)求向量
的最小值; (Ⅱ)求向量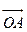 与向量
与向量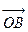 的夹角(O是坐标原点);(Ⅲ)在
的夹角(O是坐标原点);(Ⅲ)在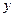 轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与
轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与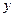 轴交于点E,且有
轴交于点E,且有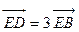 ?若存在,求出N点坐标;若不存在,说明理由.
?若存在,求出N点坐标;若不存在,说明理由.
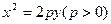 ,A,B是抛物线C上的两点,直线AB过点M
,A,B是抛物线C上的两点,直线AB过点M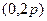 。(Ⅰ)设
。(Ⅰ)设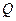 是抛物线上任意一点,求
是抛物线上任意一点,求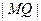 的最小值; (Ⅱ)求向量
的最小值; (Ⅱ)求向量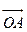 与向量
与向量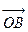 的夹角(O是坐标原点);(Ⅲ)在
的夹角(O是坐标原点);(Ⅲ)在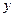 轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与
轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与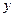 轴交于点E,且有
轴交于点E,且有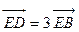 ?若存在,求出N点坐标;若不存在,说明理由.
?若存在,求出N点坐标;若不存在,说明理由.(Ⅰ)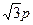 (Ⅱ)
(Ⅱ)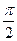 (Ⅲ)N
(Ⅲ)N
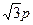 (Ⅱ)
(Ⅱ)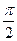 (Ⅲ)N
(Ⅲ)N
(Ⅰ)设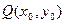 ,
,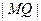
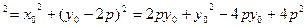
=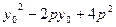
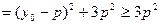 ,则
,则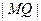 的最小值为
的最小值为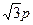 …3分
…3分
(Ⅱ)由题意可设直线AB的方程为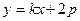 (
(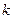 存在),令A
存在),令A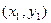 、B
、B ,将直线方程
,将直线方程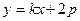 代入抛物线方程
代入抛物线方程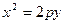 ,化简得:
,化简得: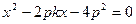 ,
,
则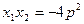 ,…5分而
,…5分而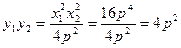 ,
,
于是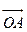
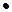
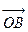 =
=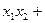
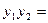
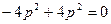 ,因此,向量
,因此,向量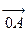 与向量
与向量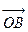 的夹角为
的夹角为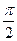 …8分
…8分
(Ⅲ)设存在点N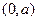 满足题意,则直线AD方程可设为
满足题意,则直线AD方程可设为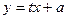 (
(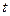 存在),
存在),
令D(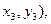 E
E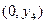 ,将直线AD方程
,将直线AD方程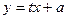
代入抛物线方程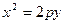 并化简得:
并化简得: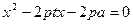 ,则
,则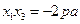 (1)………10分
(1)………10分
由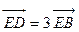 ,得(
,得(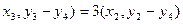 ,
,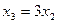 代入(1)式得
代入(1)式得
3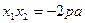 ,又由(Ⅰ)得
,又由(Ⅰ)得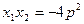 ,所以
,所以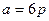 …12分
…12分
即在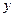 轴上存在异于M的一点N
轴上存在异于M的一点N ,使得
,使得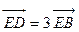 ……13分
……13分
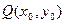 ,
,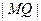
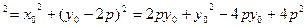
=
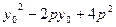
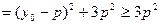 ,则
,则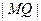 的最小值为
的最小值为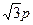 …3分
…3分(Ⅱ)由题意可设直线AB的方程为
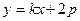 (
(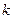 存在),令A
存在),令A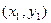 、B
、B ,将直线方程
,将直线方程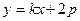 代入抛物线方程
代入抛物线方程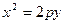 ,化简得:
,化简得: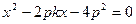 ,
,则
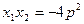 ,…5分而
,…5分而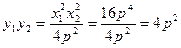 ,
,于是
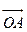
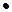
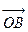 =
=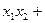
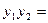
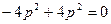 ,因此,向量
,因此,向量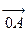 与向量
与向量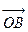 的夹角为
的夹角为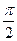 …8分
…8分(Ⅲ)设存在点N
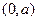 满足题意,则直线AD方程可设为
满足题意,则直线AD方程可设为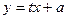 (
(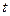 存在),
存在),令D(
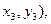 E
E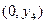 ,将直线AD方程
,将直线AD方程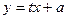
代入抛物线方程
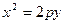 并化简得:
并化简得: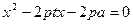 ,则
,则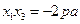 (1)………10分
(1)………10分由
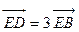 ,得(
,得(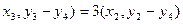 ,
,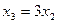 代入(1)式得
代入(1)式得3
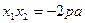 ,又由(Ⅰ)得
,又由(Ⅰ)得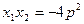 ,所以
,所以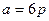 …12分
…12分即在
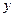 轴上存在异于M的一点N
轴上存在异于M的一点N ,使得
,使得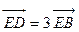 ……13分
……13分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
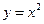 和三个点
和三个点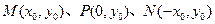
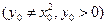 ,过点
,过点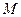 的一条直线交抛物线于
的一条直线交抛物线于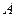 、
、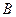 两点,
两点,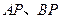 的延长线分别交曲线
的延长线分别交曲线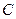 于
于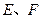 .
.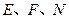 三点共线;
三点共线;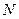 四点共线,问:是否存在
四点共线,问:是否存在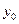 ,使以线段
,使以线段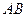 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于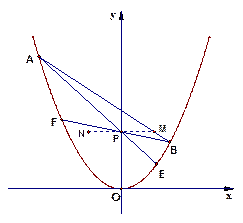
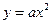 的焦点坐标为
的焦点坐标为 ,则实数
,则实数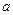 的值为 .
的值为 .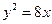 的焦点作倾斜角为
的焦点作倾斜角为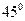 直线
直线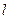 ,直线
,直线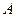 ,
,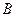 两点,则弦
两点,则弦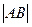 的长是( )
的长是( )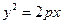 的焦点与椭圆
的焦点与椭圆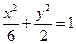 的右焦点重合,则
的右焦点重合,则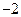 的值为( ﹡ )
的值为( ﹡ )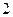
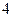
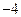
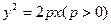 的焦点F的直线l交
的焦点F的直线l交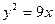
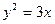
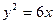
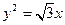
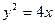 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若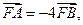 则直线AB的斜率为 ( )
则直线AB的斜率为 ( )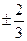 B.
B.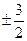 C.
C.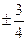 D.
D.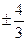
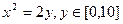 ,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为
,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 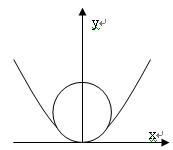
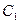 :
: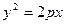 和圆
和圆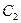 :
: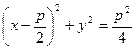 ,其中
,其中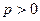 ,直线
,直线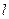 经过
经过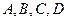 四点,则
四点,则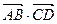 的值为 ( )
的值为 ( )