题目内容
4. 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0 交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0 交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.(1)若直线AB过焦点F,求|AF|•|BF|的值;
(2)是否存在实数p,使△ABQ是以Q为直角顶点的直角三角形?若存在,求出p的值;若不存在,说明理由.
分析 (1)抛物线的焦点坐标F(0,2),求出抛物线方程,与直线方程联立,A(x1,y1),B(x2,y2)利用韦达定理求解|AF|•|BF|的值.
(2)通过抛物线x2=2py与直线y=2x+2联立方程组,A(x1,y1),B(x2,y2),利用韦达定理以及向量的数量积,化简求解即可.
解答 解:(1)直线2x-y+2=0 交抛物线C于A、B两点,x=0,可得y=2,所以F(0,2),p=4,
抛物线x2=8y与直线y=2x+2联立方程组得:x2-16x-16=0,
A(x1,y1),B(x2,y2),
x1+x2=16,x1x2=-16,
|AF||BF|=(y1+2)(y2+2)=(2x1+4)(2x2+4)=80;(7分)
(2)假设存在,抛物线x2=2py与直线y=2x+2联立方程组得:x2-4px-4p=0,
A(x1,y1),B(x2,y2),x1+x2=4p,x1x2=-4p.
P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q,可得Q(2p,2p).
$\overrightarrow{QA}•\overrightarrow{QB}=0$得:(x1-2p)(x2-2p)+(y1-2p)(y2-2p)=0,
(x1-2p)(x2-2p)+(2x1+2-2p)(x2+2-2p)=0,
$5{x_1}{x_2}+(4-6p)({x_1}+{x_2})+8{p^2}-8p+4=0$
代入得4p2+3p-1=0,
$p=\frac{1}{4}或p=-1(舍)$(15分)
点评 本题考查直线与抛物线的位置关系的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
7.函数f(x)=$\frac{2co{s}^{2}(x-1)-x}{x-1}$,其图象的对称中心是( )
| A. | (-1,1) | B. | (1,-1) | C. | (0,1) | D. | (0,-1) |
11.设集合A={x|x2+x-6≤0},集合B为函数$y=\frac{1}{{\sqrt{x-1}}}$的定义域,则A∩B=( )
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
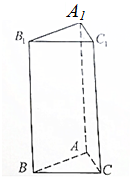 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,底面ABC为正三角形,AA1=4,BC=2,延长AB至D,使BD=AB.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,底面ABC为正三角形,AA1=4,BC=2,延长AB至D,使BD=AB.