题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合).已知
是椭圆上一动点(与左、右顶点不重合).已知![]() 的面积的最大值为
的面积的最大值为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
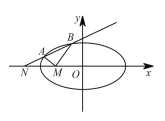
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 、
、![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由已知条件得出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 的值,进而可得出椭圆
的值,进而可得出椭圆![]() 的方程;
的方程;
(2)由题意可知直线![]() 的斜率存在,可设直线
的斜率存在,可设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,列出韦达定理,利用弦长公式求出
的方程与椭圆的方程联立,列出韦达定理,利用弦长公式求出![]() ,利用线段
,利用线段![]() 和
和![]() 的垂直平分线的交点得出点
的垂直平分线的交点得出点![]() 的坐标,进而得出
的坐标,进而得出![]() ,再对
,再对![]() 进行化简即可.
进行化简即可.
(1)![]() 的面积的最大值为
的面积的最大值为![]() ,
,
由已知条件得 ,解得
,解得 ,因此,椭圆
,因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意可知,直线![]() 的斜率存在,且不为零,易知点
的斜率存在,且不为零,易知点![]() ,
,
设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,可知点
,可知点![]() ,
,
联立 ,消去
,消去![]() 得
得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
由弦长公式得
![]() ,
,
![]() ,
,![]() ,
,
所以,线段![]() 的中点为
的中点为 ,
,
则线段![]() 的垂直平分线的方程为
的垂直平分线的方程为 ,即
,即![]() ,
,
线段![]() 的垂直平分线为
的垂直平分线为![]() 轴,在直线方程
轴,在直线方程![]() 中,令
中,令![]() ,得
,得![]() .
.
则点 ,
, ,
,
因此, (定值).
(定值).

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是2019年我国某地区新能源乘用车的前5个月销售量与月份的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 |
销售量 | 0.5 | 0.6 | 1 | 1.4 | 1.5 |
(1)利用线性相关系数![]() 判断
判断![]() 与
与![]() 的线性相关性,并求出线性回归方程
的线性相关性,并求出线性回归方程
(2)根据线性回归方程预报2019年6月份的销售量约为多少万辆?
参考公式: ,
,![]() ;回归直线:
;回归直线:![]() .
.
 ,
,![]()
【题目】为了解高一年级学生的智力水平,某校按1:10的比例对700名高一学生按性别分别进行“智力评分”抽样调查,测得“智力评分”的频数分布表如表1、表2所示.
表1:男生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |

(1)求高一年级的男生人数,并完成下面男生“智力评分”的频率分布直方图;
(2)估计该校高一年级学生“智力评分”在![]() 内的人数.
内的人数.
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?