题目内容
已知数列{an}满足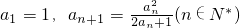
(I)求a2,a3的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)记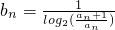 ,若对于任意正整数n都有
,若对于任意正整数n都有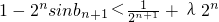 成立,求实数λ的取值范围.
成立,求实数λ的取值范围.
解:(I)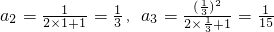
(Ⅱ)原式两边取倒数,则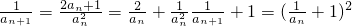
上式两边取对数,则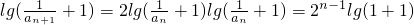
解得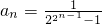
(Ⅲ)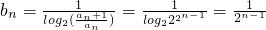
由题中不等式解得,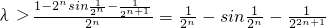 对于任意正整数均成立
对于任意正整数均成立
注意到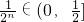 ,构造函数
,构造函数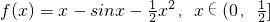
则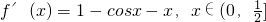 设函数
设函数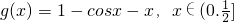
由g'(x)=sinx-1<0对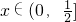 成立,得g(x)=1-cosx-x为
成立,得g(x)=1-cosx-x为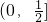 上的减函数,
上的减函数,
所以g(x)max<g(0)=0即f'(x)<0对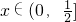 成立,因此f(x)为
成立,因此f(x)为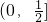 上的减函数,
上的减函数,
即f(x)max<f(0)=0,故λ≥0
分析:(I)直接利用递推公式,令n=1,n=2计算
(Ⅱ)原式两边取倒数,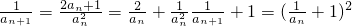 ,再取对数,构造出
,再取对数,构造出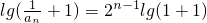 .据此求{an}的通项公式;
.据此求{an}的通项公式;
(Ⅲ)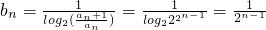 ,分离常数,变为λ>y 恒成立的形式,故λ大于y的最大值,利用y 的单调性确定它的最大值.
,分离常数,变为λ>y 恒成立的形式,故λ大于y的最大值,利用y 的单调性确定它的最大值.
点评:本题主要考查数列通项公式求解、不等式恒成立问题.用到对数的运算、函数与导数知识,需具有转化构造能力、计算能力、分析解决问题能力.
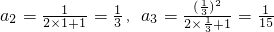
(Ⅱ)原式两边取倒数,则
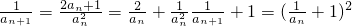
上式两边取对数,则
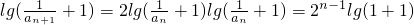
解得
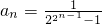
(Ⅲ)
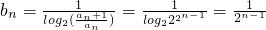
由题中不等式解得,
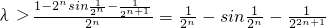 对于任意正整数均成立
对于任意正整数均成立注意到
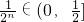 ,构造函数
,构造函数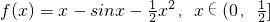
则
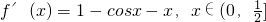 设函数
设函数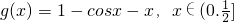
由g'(x)=sinx-1<0对
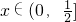 成立,得g(x)=1-cosx-x为
成立,得g(x)=1-cosx-x为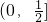 上的减函数,
上的减函数,所以g(x)max<g(0)=0即f'(x)<0对
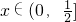 成立,因此f(x)为
成立,因此f(x)为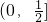 上的减函数,
上的减函数,即f(x)max<f(0)=0,故λ≥0
分析:(I)直接利用递推公式,令n=1,n=2计算
(Ⅱ)原式两边取倒数,
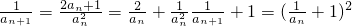 ,再取对数,构造出
,再取对数,构造出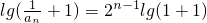 .据此求{an}的通项公式;
.据此求{an}的通项公式;(Ⅲ)
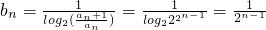 ,分离常数,变为λ>y 恒成立的形式,故λ大于y的最大值,利用y 的单调性确定它的最大值.
,分离常数,变为λ>y 恒成立的形式,故λ大于y的最大值,利用y 的单调性确定它的最大值.点评:本题主要考查数列通项公式求解、不等式恒成立问题.用到对数的运算、函数与导数知识,需具有转化构造能力、计算能力、分析解决问题能力.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目