题目内容
(本小题满分14分)
执行下面框图所描述的算法程序,记输出的一列数依次为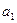 ,
,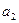 ,…,
,…, ,
, ,
,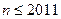 .(注:框图中的赋值符号“
.(注:框图中的赋值符号“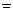 ”也可以写成“
”也可以写成“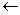 ”或“:
”或“: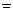 ”)
”)
(1)若输入 ,写出输出结果;
,写出输出结果;
(2)若输入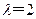 ,求数列
,求数列 的通项公式;
的通项公式;
(3)若输入 ,令
,令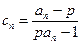 ,求常数
,求常数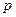 (
(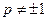 ),使得
),使得 是等比数列.
是等比数列.
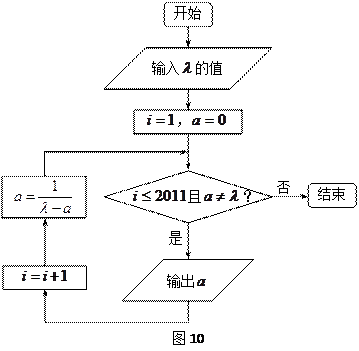
执行下面框图所描述的算法程序,记输出的一列数依次为
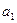 ,
,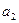 ,…,
,…, ,
, ,
,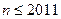 .(注:框图中的赋值符号“
.(注:框图中的赋值符号“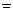 ”也可以写成“
”也可以写成“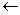 ”或“:
”或“: ”)
”)(1)若输入
 ,写出输出结果;
,写出输出结果;(2)若输入
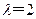 ,求数列
,求数列 的通项公式;
的通项公式;(3)若输入
 ,令
,令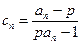 ,求常数
,求常数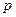 (
(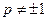 ),使得
),使得 是等比数列.
是等比数列.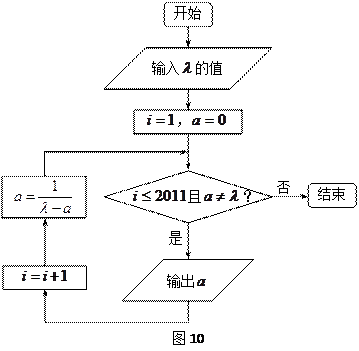
解(1)输出结果是:0,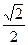 ,
,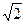 .……3分
.……3分
(2)(法一)由程序框图可知,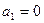 ,
,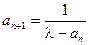 ,
, ,
,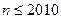 .
.
所以,当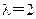 时,
时,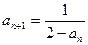 , …………………5分
, …………………5分
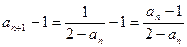 ,而
,而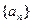 中的任意一项均不为1,(否则的话,由
中的任意一项均不为1,(否则的话,由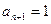 可以得到
可以得到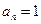 ,…,与
,…,与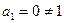 矛盾),
矛盾),
所以,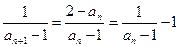 ,
,
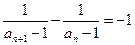 (常数),
(常数), ,
,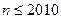 .故
.故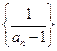 是首项为
是首项为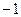 ,公差为
,公差为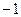 的等差数列, ……………………………7分
的等差数列, ……………………………7分
所以,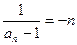 ,数列
,数列 的通项公式为
的通项公式为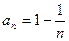 ,
, ,
,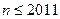 .…8分
.…8分
(法二)当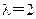 时,由程序框图可知,
时,由程序框图可知,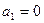 ,
,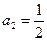 ,
,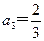 ,
,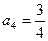 ,……
,……
猜想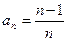 ,
, ,
,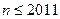 . …………………………………………5分
. …………………………………………5分
以下用数学归纳法证明:
①当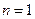 时,
时,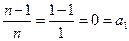 ,猜想正确;
,猜想正确;
②假设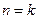 (
( ,
,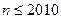 )时,猜想正确.即
)时,猜想正确.即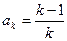 ,………………7分
,………………7分
那么,当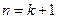 时,
时,
由程序框图可知,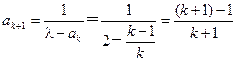 .即
.即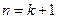 时,猜想也正确.
时,猜想也正确.
由①②,根据数学归纳法原理,猜想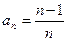 正确,
正确, ,
,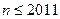 .……8分
.……8分
(3)(法一)当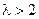 时,
时,
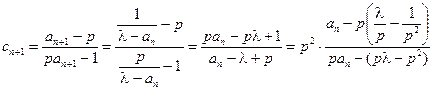 ,
,
令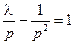 ,则
,则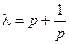 ,
,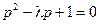 ,
,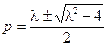 . …………10分
. …………10分
此时,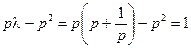 , ………………………………12分
, ………………………………12分
所以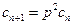 ,
, ,
,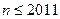 ,又
,又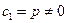 ,
,
故存在常数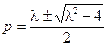 (
(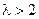 ),
),
使得 是以
是以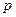 为首项,
为首项,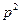 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分
(法二)当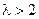 时,令
时,令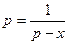 ,即
,即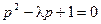 ,解得
,解得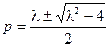 ,…10分
,…10分
因为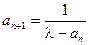 ,
, ,
,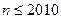 .
.
所以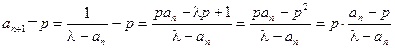 , ①
, ①
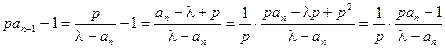 ,② 12分
,② 12分
①÷②,得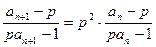 ,
,
即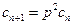 ,
, ,
,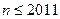 ,又
,又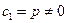 ,
,
故存在常数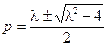 (
(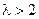 )
)
使得 是以
是以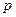 为首项,
为首项,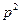 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分
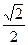 ,
,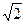 .……3分
.……3分(2)(法一)由程序框图可知,
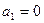 ,
,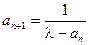 ,
, ,
,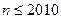 .
.所以,当
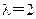 时,
时,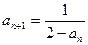 , …………………5分
, …………………5分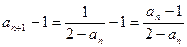 ,而
,而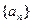 中的任意一项均不为1,(否则的话,由
中的任意一项均不为1,(否则的话,由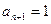 可以得到
可以得到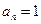 ,…,与
,…,与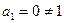 矛盾),
矛盾),所以,
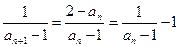 ,
,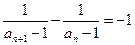 (常数),
(常数), ,
,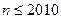 .故
.故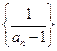 是首项为
是首项为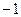 ,公差为
,公差为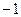 的等差数列, ……………………………7分
的等差数列, ……………………………7分所以,
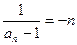 ,数列
,数列 的通项公式为
的通项公式为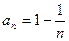 ,
, ,
,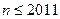 .…8分
.…8分(法二)当
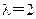 时,由程序框图可知,
时,由程序框图可知,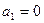 ,
,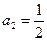 ,
,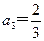 ,
,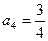 ,……
,……猜想
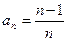 ,
, ,
,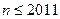 . …………………………………………5分
. …………………………………………5分以下用数学归纳法证明:
①当
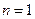 时,
时,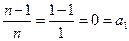 ,猜想正确;
,猜想正确;②假设
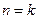 (
( ,
,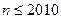 )时,猜想正确.即
)时,猜想正确.即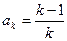 ,………………7分
,………………7分那么,当
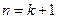 时,
时,由程序框图可知,
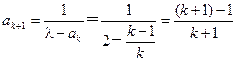 .即
.即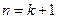 时,猜想也正确.
时,猜想也正确.由①②,根据数学归纳法原理,猜想
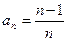 正确,
正确, ,
,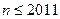 .……8分
.……8分(3)(法一)当
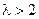 时,
时,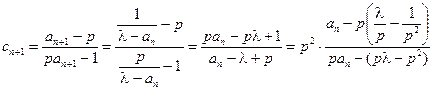 ,
,令
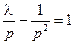 ,则
,则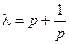 ,
,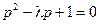 ,
,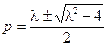 . …………10分
. …………10分此时,
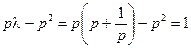 , ………………………………12分
, ………………………………12分所以
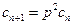 ,
, ,
,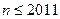 ,又
,又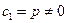 ,
,故存在常数
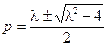 (
(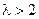 ),
),使得
 是以
是以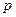 为首项,
为首项,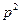 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分(法二)当
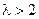 时,令
时,令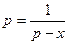 ,即
,即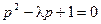 ,解得
,解得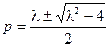 ,…10分
,…10分因为
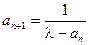 ,
, ,
,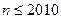 .
.所以
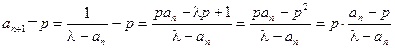 , ①
, ①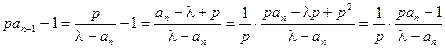 ,② 12分
,② 12分①÷②,得
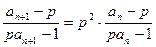 ,
,即
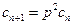 ,
, ,
,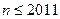 ,又
,又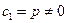 ,
,故存在常数
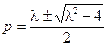 (
(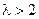 )
)使得
 是以
是以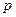 为首项,
为首项,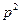 为公比的等比数列. ……………………………14分
为公比的等比数列. ……………………………14分略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
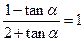 ,求证
,求证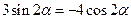
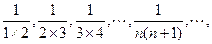 计算
计算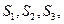 由此推算
由此推算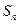 的公式,并用数学归纳法给出证明。
的公式,并用数学归纳法给出证明。 1=c,2Sn=anan+1+r.
1=c,2Sn=anan+1+r. 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由. ,
, ,
,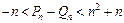 恒成立.
恒成立. 中,
中,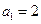 ,
,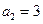 ,其前
,其前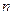 项和
项和 满足
满足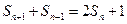 (
(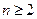 ,
,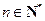 ).
).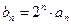 ,求数列
,求数列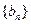 的前
的前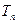 ;
;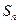 为数列
为数列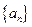 的前
的前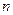 项和,且
项和,且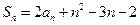 ,
,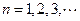 ,
,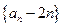 为等比数列;
为等比数列;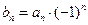 ,求数列
,求数列 的前
的前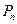 ;
;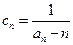 ,数列
,数列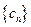 的前
的前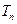 ,求证:
,求证: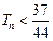 .
.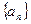 的前
的前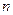 项和
项和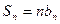 ,其中
,其中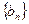 是首项为
是首项为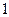 ,公差为
,公差为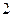 的等差数列.
的等差数列.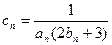 ,求数列
,求数列
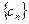 的前
的前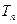 .
. 0年举办第四届),下表列出了1974年联邦德国第十届世界杯足球赛以来的几届世界杯举办地:
0年举办第四届),下表列出了1974年联邦德国第十届世界杯足球赛以来的几届世界杯举办地: 18
18
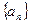 、
、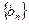 都是等
都是等 差数列,且
差数列,且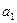 =5,
=5,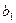 =15,
=15,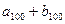 =100,则数列
=100,则数列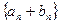 的前
的前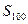 等于: ( )
等于: ( ) 、 6000 D、60000
、 6000 D、60000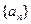 中,若点
中,若点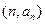 在经过点(5,3)的定直线l上,则数列
在经过点(5,3)的定直线l上,则数列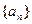 的前9项和S9=" " .
的前9项和S9=" " .