题目内容
称一个函数是“好函数”当且仅当其满足: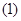 定义在
定义在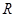 上;
上;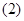 存在
存在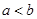 ,使其在
,使其在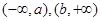 上单调递增,在
上单调递增,在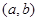 上单调递减,则以下函数是“好函数”的有 .
上单调递减,则以下函数是“好函数”的有 .
?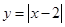 ;?
;?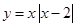 ;?
;?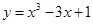 ;④
;④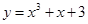
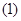 定义在
定义在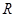 上;
上;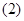 存在
存在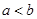 ,使其在
,使其在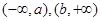 上单调递增,在
上单调递增,在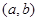 上单调递减,则以下函数是“好函数”的有 .
上单调递减,则以下函数是“好函数”的有 .?
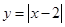 ;?
;?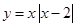 ;?
;?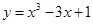 ;④
;④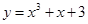
.②③
试题分析:解:①中函数y=|x-2|定义域为R,y=|x-2|=
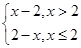 ∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;②中函数y=x|x-2|定义域为R,y=x|x-2|=
∴不存在a,使y=|x-2|在(-∞,a)上单调递增,故不正确;②中函数y=x|x-2|定义域为R,y=x|x-2|=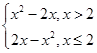 y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-
y=x|x-2|在(-∞,1)、(2,+∞)上单调递增,在(1,2)上单调递减,满足好函数的定义,故正确;③中函数y=x3-x+1定义域为R,则y′=3x2-1<0解得x∈(-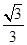 ,
,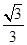 ),y′=3x2-1>0解得x∈(-∞,-
),y′=3x2-1>0解得x∈(-∞,-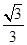 )∪(
)∪(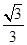 ,+∞),∴y=x3-x+1在(-∞,-
,+∞),∴y=x3-x+1在(-∞,-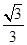 )、(
)、(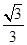 ,+∞)上单调递增,在(-
,+∞)上单调递增,在(-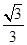 ,
,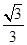 )上单调递减,满足好函数的定义,故正确;④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立,故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;故答案为:②③
)上单调递减,满足好函数的定义,故正确;④中函数y=x3+x+3定义域为R,则y′=3x2+1>0恒成立,故不存在a<b,使函数y=x3+x+3在(a,b)上单调递减,不满足好函数的定义,故不正确;故答案为:②③点评:本题主要考查了利用导数研究函数的单调性,以及绝对值函数的处理方法和新定义,同时考查了转化的思想,属于中档题

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
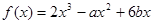 在
在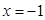 处有极大值7.
处有极大值7.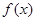 的解析式;(Ⅱ)求
的解析式;(Ⅱ)求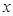 =1处的切线方程.
=1处的切线方程.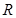 上的周期函数
上的周期函数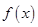 ,其周期
,其周期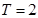 ,直线
,直线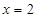 是它的图象的一条对称轴,且
是它的图象的一条对称轴,且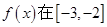 上是减函数.如果
上是减函数.如果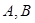 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )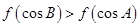

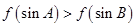
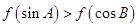
 万元满足
万元满足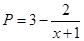 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为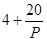 元.
元.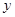 万元表示为促销费用
万元表示为促销费用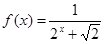 ,利用课本中推导等差数列前n项和公式的方法,可求得
,利用课本中推导等差数列前n项和公式的方法,可求得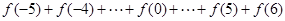 的值 。
的值 。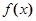 是一次函数,其图像过点
是一次函数,其图像过点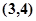 ,且
,且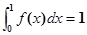 ,求
,求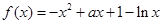
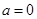 ,求在
,求在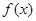 图象与
图象与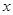 轴交点处的切线方程;
轴交点处的切线方程;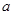 的范围.
的范围.